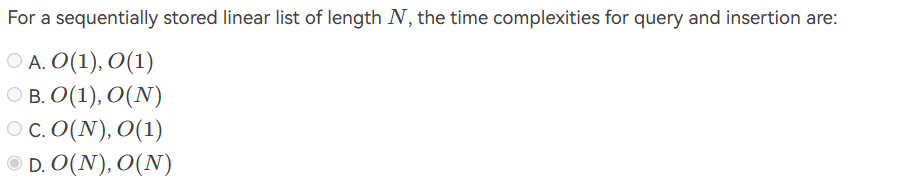数据结构与算法基础
fds
说明
本网站的一些知识总结引用了一些前辈的内容,在此感谢前辈们的资料的整理!!!
算法分析基础
基础数据结构:链表、栈、队列
链表
- 链表是一种常见的数据结构,它的元素可以存储在内存的任何位置。每个元素(通常称为节点)都包含两个部分:一个是存储的数据,另一个是指向下一个节点的引用(在C语言中称为指针)。
- 链表有多种类型,包括单向链表、双向链表和循环链表。
- 单向链表只能向一个方向遍历,每个节点只有指向下一个节点的链接。
双向链表的每个节点都有两个链接,一个指向前一个节点,另一个指向后一个节点。 - 循环链表是一种特殊类型的链表,其中最后一个元素指向第一个元素,形成一个闭环。
栈和队列
- 栈是一种特殊的线性表
- 它的操作仅仅在线性表的一端进行,而在另一端无法进行
- push 和 pop 两个典型操作
1 | |
一些小坑
在正式进行作业时,我用数组模拟栈进行编程,但是很多时候一定要注意循环结构结束导致模拟栈数组的边界问题(很容易错喵);
此外有些时候OJ对于局部变量用在全局时会将原本存储在系统中的值直接使用,常常发现有奇怪的数据
栈的应用
计算器的设计
1 | |
fds小题杂题
算法分析(chapter 2)
时间复杂度
![time]()
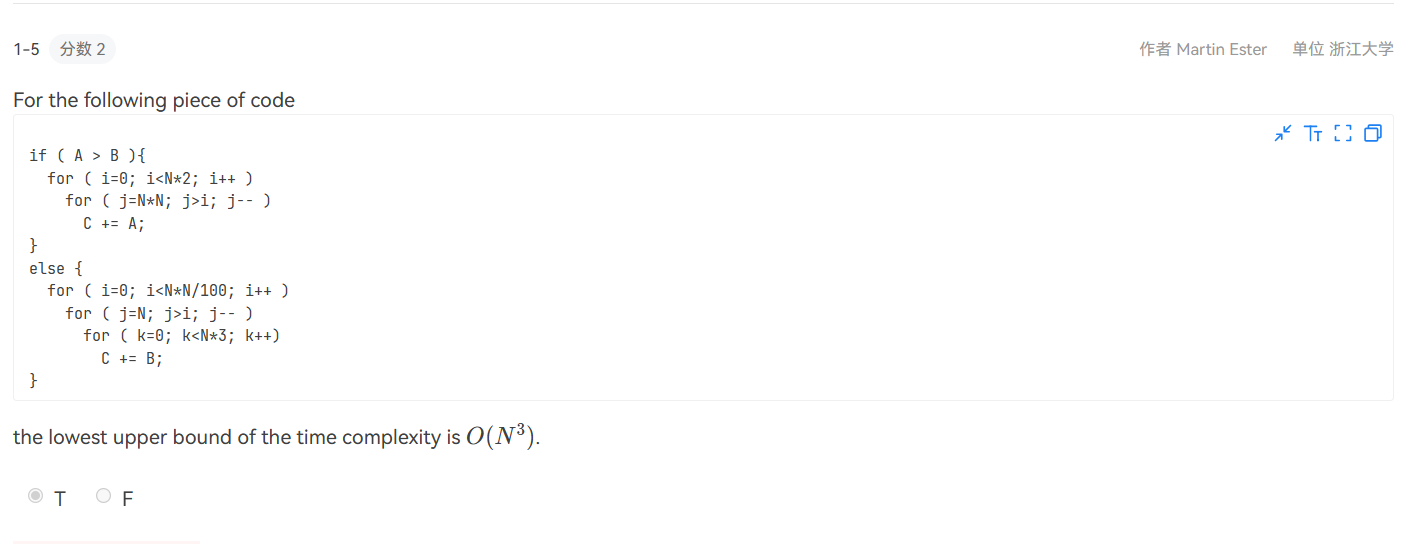
ex1(分析时间复杂度)
![ex1]()
分析:首先要搞懂英文的含义,最小的时间上限。则由数学知识可知:O(N)=$\sum_{i=0}^{2*n}$ $\sum_{i=1}^{n}$
基本数据结构喵(chapter 3)
一些补充内容
- 在链表结构中,头指针是一个特殊的指针,其主要功能是存储链表的起始地址。
- 链表是由一组节点构成,每个节点包含数据元素和指向下一个节点的指针。链表的第一个节点被称为头节点(head pointer)。对于链表的访问,一般都是通过头指针来进行的,因为只有头指针记录了链表的起始地址,进而我们可以通过头指针逐个访问链表中的每一个节点。
- 注意:头指针与头节点虽然经常一起被提起,然而是两个不同的概念。头节点指的是链表中的第一个节点,而头指针指的是指向头节点的指针。有时候,为了方便对链表的操作,也会创建一个带有空数据域的”头节点”(dummy header),这种情况下的”头指针”就会指向这个不存储具体数据的节点。
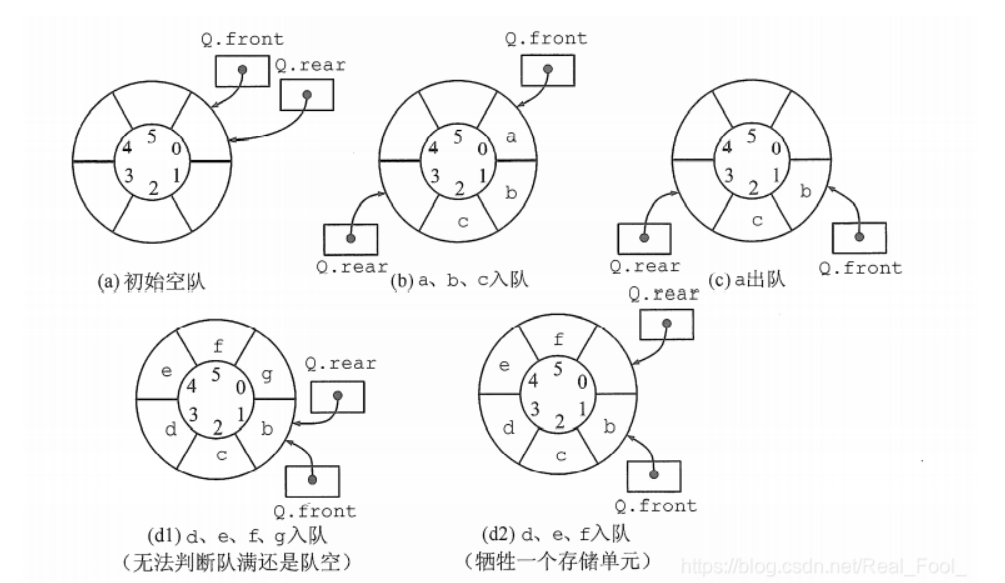
- 循环队列
![xunhuan]()
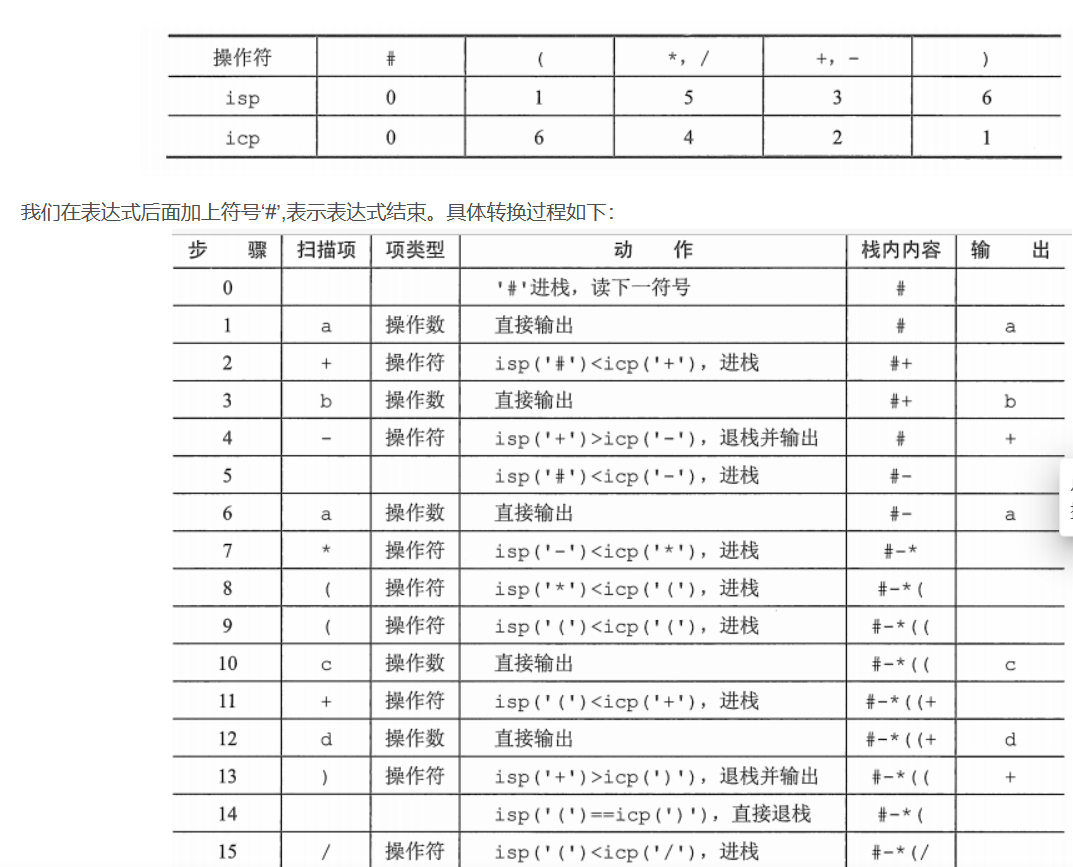
中缀表达式转化为后缀表达式
具体操作步骤:
- 初始化两个栈:运算符栈S1;操作数栈S2
- 从左向右扫描中缀表达式
- 遇到操作数时,将其压入到操作数栈S2
- 遇到运算符时,比较其与运算符栈S1栈顶运算符的优先级
- 如果运算符栈S1为空,或栈顶运算符为左括号“ ( ”,或者优先级比栈顶运算符的优先级较高,则直接将此运算符压入栈中(三种情况:空、左、高)
- 否则,将运算符栈S1中栈顶的运算符弹入并压到操作数栈S2中,再次进行与运算符栈S1栈顶运算符的优先级比较
- 遇到括号时,如果遇到了左括号“ ( ”,则直接压入运算符栈S1;
- 如果遇到右括号“ ) ”,则依次弹出运算符栈S1栈顶的运算符,并压入操作数栈S2,直到遇到左括号” ( “为止,此时将这一对括号丢弃
重复步骤2至8,直到表达式的最右边
将运算符栈S1剩余的运算符依次弹出并压入操作数栈S2
- 促进记忆表达式树
表达式树的先根遍历:前缀表达式
表达式树的中根遍历:中缀表达式
表达式树的后根遍历:后缀表达式
基本数据结构小题
- ex1(循环队列)
![xunhuanqueue]()
补充知识点
定义:用一个数组来存储队列中的元素,用front作为队头指针,指向队列的第一个元素,用rear作为队尾指针,即指向队列最后一个元素的下一个位置.
初始化:循环队列的初始化只需要将队头指针(front)和队尾指针(rear)都初始化为0.
循环队列出队:出队前判断队列是否为空,如果为空,返回100002错误信息,如果队列不为空,将队列的队头指针向前移动一位,即将队头指针加1并对MAXSIZE取模,确保指针在数组范围内循环移动,当到达数组末尾时,会回到数组的开头。
入队:入队前需要判断队列是否已经满了,如果队列为满,则不能入队。反之,则将队列的队尾向前移动一位,确保指针在数组范围内能够循环移动。具体来说,就是将当前队尾指针的值加1,然后对队列的最大容量(MAXSIZE)取模来实现。
解析:根据定义可解决上述问题。
ex2(在HW3中还有一道题目需要你们仔细读题,tmd(bushi):cry:,考视力啊)
ex3(linked list)
![linkedlist]()
ex4(sequential list)
![sequential]()
解析:需要关注的是插入并不知道具体位置在何处,所以应该是线性的时间,并且有基本概念,确实符合O(N)
- ex5(蚌埠住了(我承认我没看懂))
![bengbuzhu]()
树(chapter 4)
树的具体知识点
定义
树是n(n>=0)个结点的有限集。当n = 0时,称为空树。在任意一棵非空树中应满足:有且仅有一个特定的称为根的结点。
当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每个集合本身又是一棵树,并且称为根的子树。
显然,树的定义是递归的,即在树的定义中又用到了自身,树是一种递归的数据结构。树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
树的根结点没有前驱,除根结点外的所有结点有且只有一个前驱。
树中所有结点可以有零个或多个后继。
因此n个结点的树中有n-1条边。
基本结构
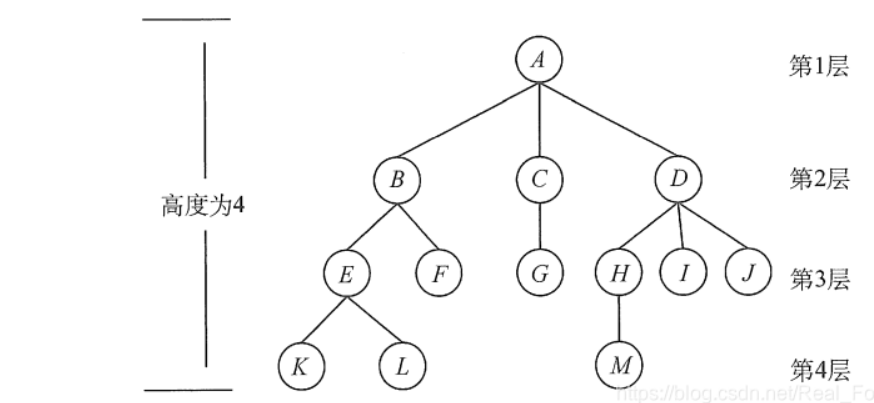
考虑结点K。根A到结点K的唯一路径上的任意结点,称为结点K的祖先(ancestor)。如结点B是结点K的祖先,而结点K是结点B的子孙(descendants)。路径上最接近结点K的结点E称为K的双亲,而K为结点E的孩子。根A是树中唯一没有双亲的结点。有相同双亲的结点称为兄弟(sibing),如结点K和结点L有相同的双亲E,即K和L为兄弟。
树中一个结点的孩子个数称为该结点的度,树中结点的最大度数称为树的度。如结点B的度为2,结点D的度为3,树的度为3。度大于0的结点称为分支结点(又称非终端结点);度为0(没有子女结点)的结点称为叶子结点(又称终端结点)。在分支结点中,每个结点的分支数就是该结点的度。
结点的深度、高度和层次。
结点的层次从树根开始定义,根结点为第1层,它的子结点为第2层,以此类推。双亲在同一层的结点互为堂兄弟,图中结点G与E,F,H,I,J互为堂兄弟。
结点的深度是从根结点开始自顶向下逐层累加的。
结点的高度是从叶结点开始自底向上逐层累加的。
树的高度(或深度)是树中结点的最大层数。图中树的高度为4。
有序树和无序树。树中结点的各子树从左到右是有次序的,不能互换,称该树为有序树,否则称为无序树。假设图为有序树,若将子结点位置互换,则变成一棵不同的树。路径和路径长度。树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的,而路径长度是路径上所经过的边的个数。
注意:由于树中的分支是有向的,即从双亲指向孩子,所以树中的路径是从上向下的,同一双亲的两个孩子之间不存在路径。森林。森林是m (m≥0)棵互不相交的树的集合。森林的概念与树的概念十分相近,因为只要把树的根结点删去就成了森林。反之,只要给m棵独立的树加上一个结点,并把这m棵树作为该结点的子树,则森林就变成了树。
树的存储结构
双亲表示法
我们假设以一组连续空间存储树的结点,同时在每个结点中,附设一个指示器指示其双亲结点到链表中的位置。也就是说,每个结点除了知道自已是谁以外,还知道它的双亲在哪里。孩子表示法
具体办法是,把每个结点的孩子结点排列起来,以单链表作存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。然后n个头指针又组成-一个线性表,采用顺序存储结构,存放进一个一维数组中.孩子兄弟表示法
刚才我们分别从双亲的角度和从孩子的角度研究树的存储结构,如果我们从树结点的兄弟的角度又会如何呢?当然,对于树这样的层级结构来说,只研究结点的兄弟是不行的,我们观察后发现,任意一棵树, 它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。 因此,我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。
二叉树
- 遍历二叉树
先序遍历(中左右)
1 | |
中序遍历(左中右)
1 | |
后序遍历(左右中)postorder
1 | |
层次遍历
1 | |
非递归前序遍历
1 | |
- 由二叉树的先序序列和中序序列可以唯一地确定一棵二叉树。
- 在先序遍历序列中,第一个结点一定是二叉树的根结点;而在中序遍历中,根结点必然将中序序列分割成两个子序列,前一个子序列是根结点的左子树的中序序列,后一个子序列是根结点的右子树的中序序列。根据这两个子序列,在先序序列中找到对应的左子序列和右子序列。在先序序列中,左子序列的第一个结点是左子树的根结点,右子序列的第一个结点是右子树的根结点。
如此递归地进行下去,便能唯一地确定这棵二叉树 - 同理,由二叉树的后序序列和中序序列也可以唯一地确定一棵二叉树。
因为后序序列的最后一个结点就如同先序序列的第一个结点,可以将中序序列分割成两个子序列,然后采用类似的方法递归地进行划分,进而得到一棵二叉树。 - 由二叉树的层序序列和中序序列也可以唯一地确定一棵二叉树。
要注意的是,若只知道二叉树的先序序列和后序序列,则无法唯一确定一棵二叉树。
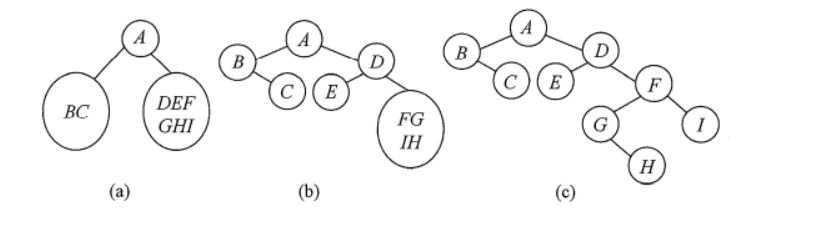
例如,求先序序列ABCDEFGH和中序序列BCAEDGHFI所确定的二叉树
首先,由先序序列可知A为二叉树的根结点。中序序列中A之前的BC为左子树的中序序列,EDGHFI为右子树的中序序列。然后由先序序列可知B是左子树的根结点,D是右子树的根结点。以此类推,就能将剩下的结点继续分解下去,最后得到的二叉树如图©所示
线索二叉树
- 我们把这种指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应的二叉树就称为线索二叉树
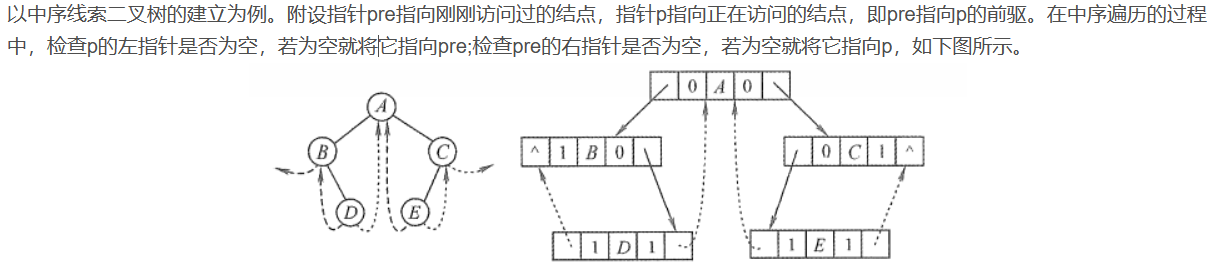
- 二叉树的线索化
二叉树的线索化是将二叉链表中的空指针改为指向前驱或后继的线索。而前驱或后继的信息只有在遍历时才能得到,因此线索化的实质就是遍历一次二叉树,线索化的过程就是在遍历的过程中修改空指针的过程 - 中序线索二叉树
![xiansuo]()
for example
1 | |
- 先序与后序
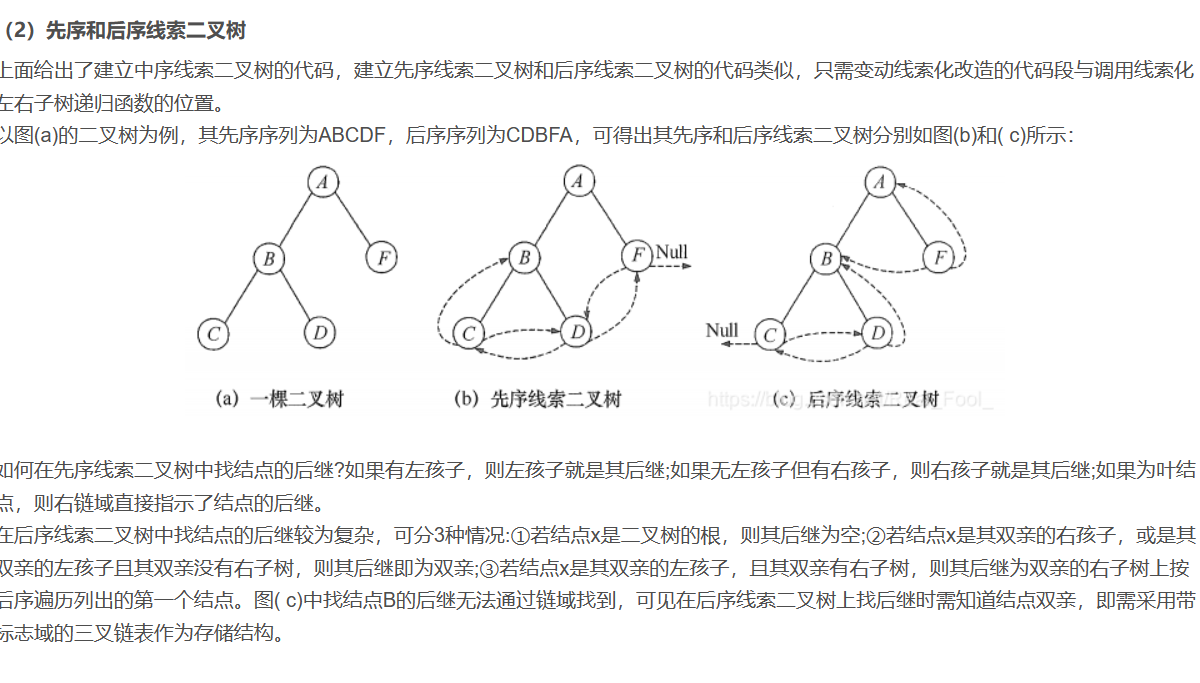
二叉查找树
- 定义:二叉排序树(也称二叉查找树)或者是一棵空树,或者是具有下列特性的二叉树:
若左子树非空,则左子树上所有结点的值均小于根结点的值。
若右子树非空,则右子树上所有结点的值均大于根结点的值。
左、右子树也分别是一棵二叉排序树。
查找
1 | |
$O(log N)$
插入
1 | |
$O(log N)$
删除
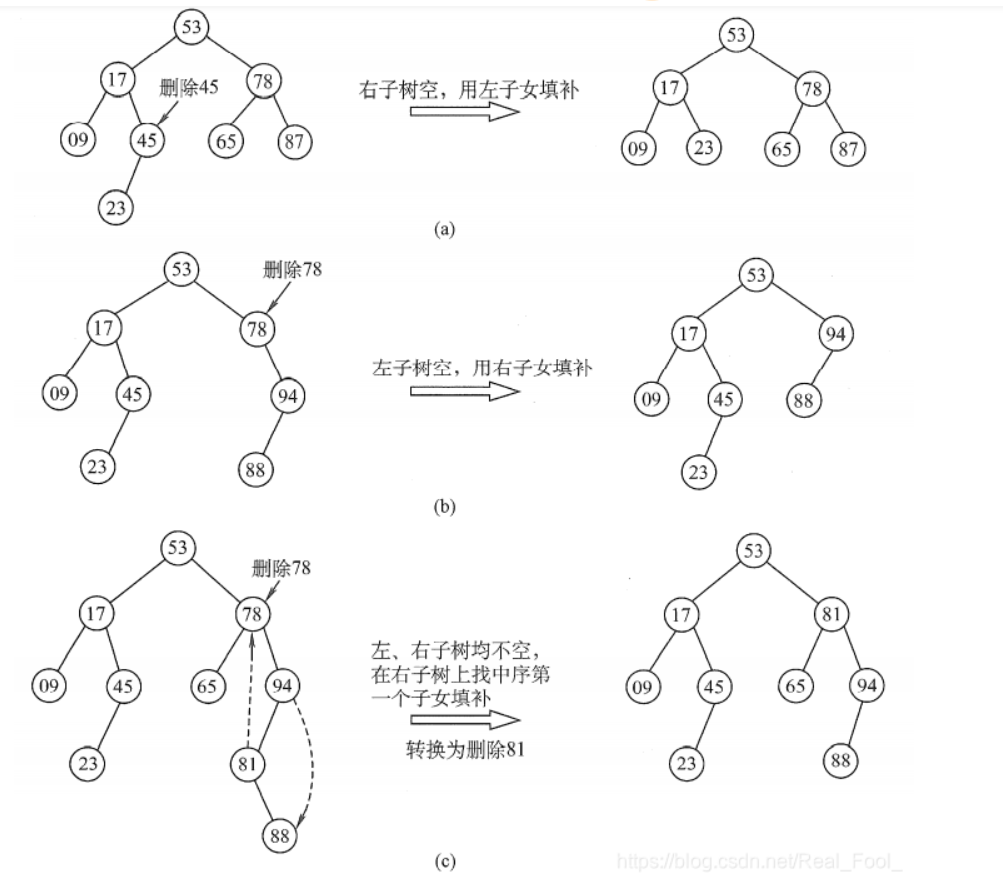
:smile:总结:对于第三种情况可以进行两种操作,用左子树最大元素或者右子树最小元素替代。
特殊树的补充
perfect tree(完美二叉树)
除了叶子结点之外,每个节点都有两个孩子,每一层(包括最后一层)都被完全填充
complete tree(完全二叉树)
除了最后一层外每一层都被完全填充,且保持左对齐
full tree(完满二叉树)
除了叶子节点之外,每个节点都有两个孩子
树的题目
- ex1(二叉查找树)
![ex1]()
解析:首先我们应注意这道题的前提是一个完全的二叉查找树,两个前提条件但是可能存在最右端的小子树的根只有左节点刚好没有右节点,则此时最大值并不在叶上。
- ex2
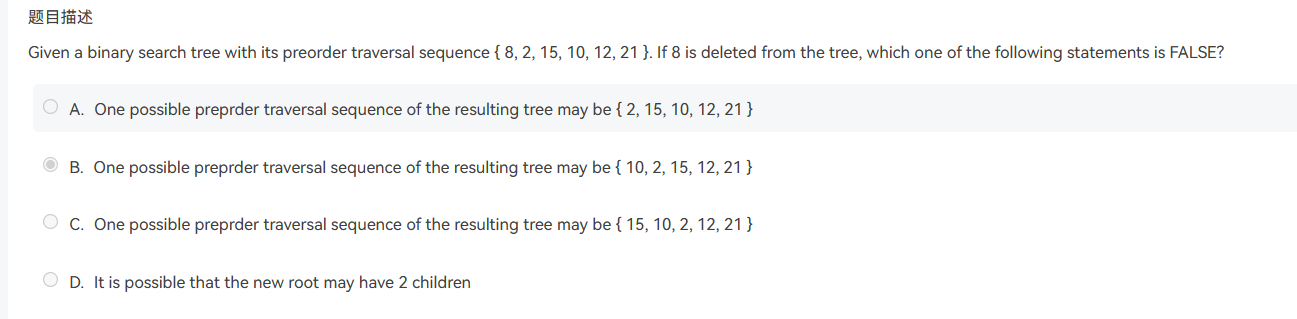
![ex2]()
importanat解析:现给定二叉查找树的先序排序,且由树的确立,可知有可能有多种情况。且对于二叉查找树如何删除节点的三种情况掌握不牢,建议再次温习知识。
- ex3(exclude):cry:重点单词exclude:排除:smile:
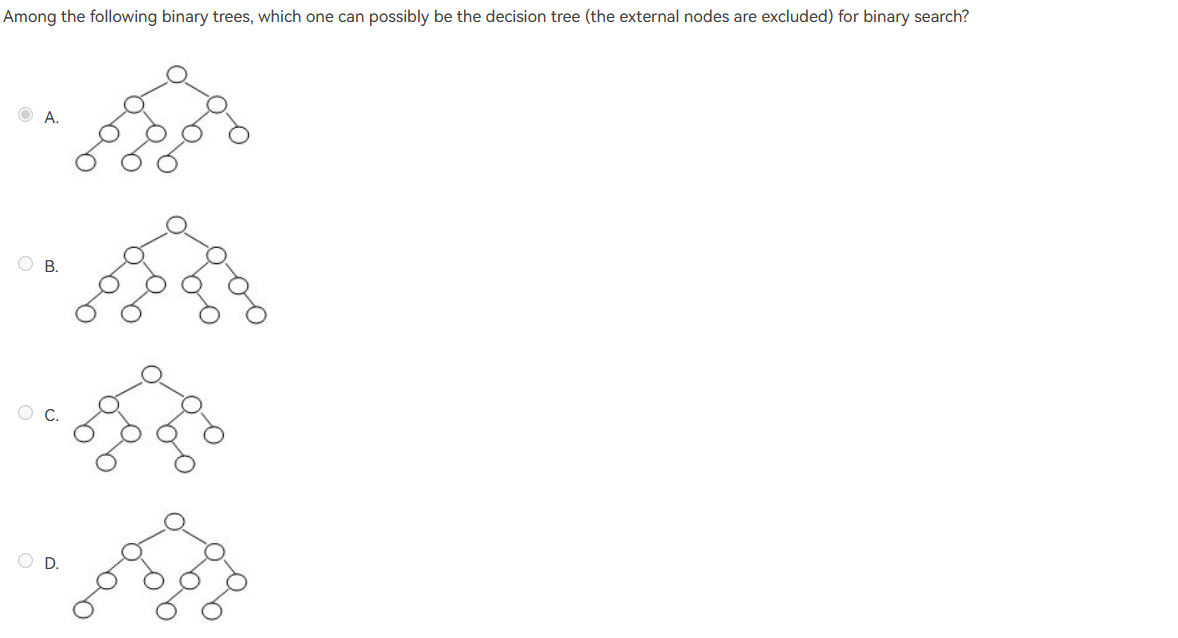
![ex3]()
important解析:这一道题我觉得较为困难,因为决策树是机器学习中的内容吧:cry:,根据各位前辈的帖子我大概可以猜测,若要是决策树的话,首先不能呈轴对称(树的形状)这样能保证上下取整的一致。其次,对于根节点,若左子树的数量多于右子树,那么每个小根的左子树的数量都应该多于右子树。
- ex4(普通树转化为二叉树)
![ex4]()
解析:最重要的关系是如何使普通树转化为二叉树,现在先给出结论:对于每个节点,其左儿子是他的第一个儿子,其右儿子是他的第一个兄弟。
下面给出例子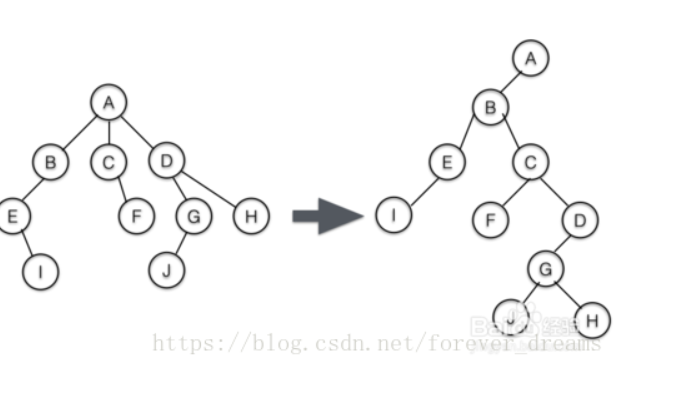
- ex5(线索二叉树)
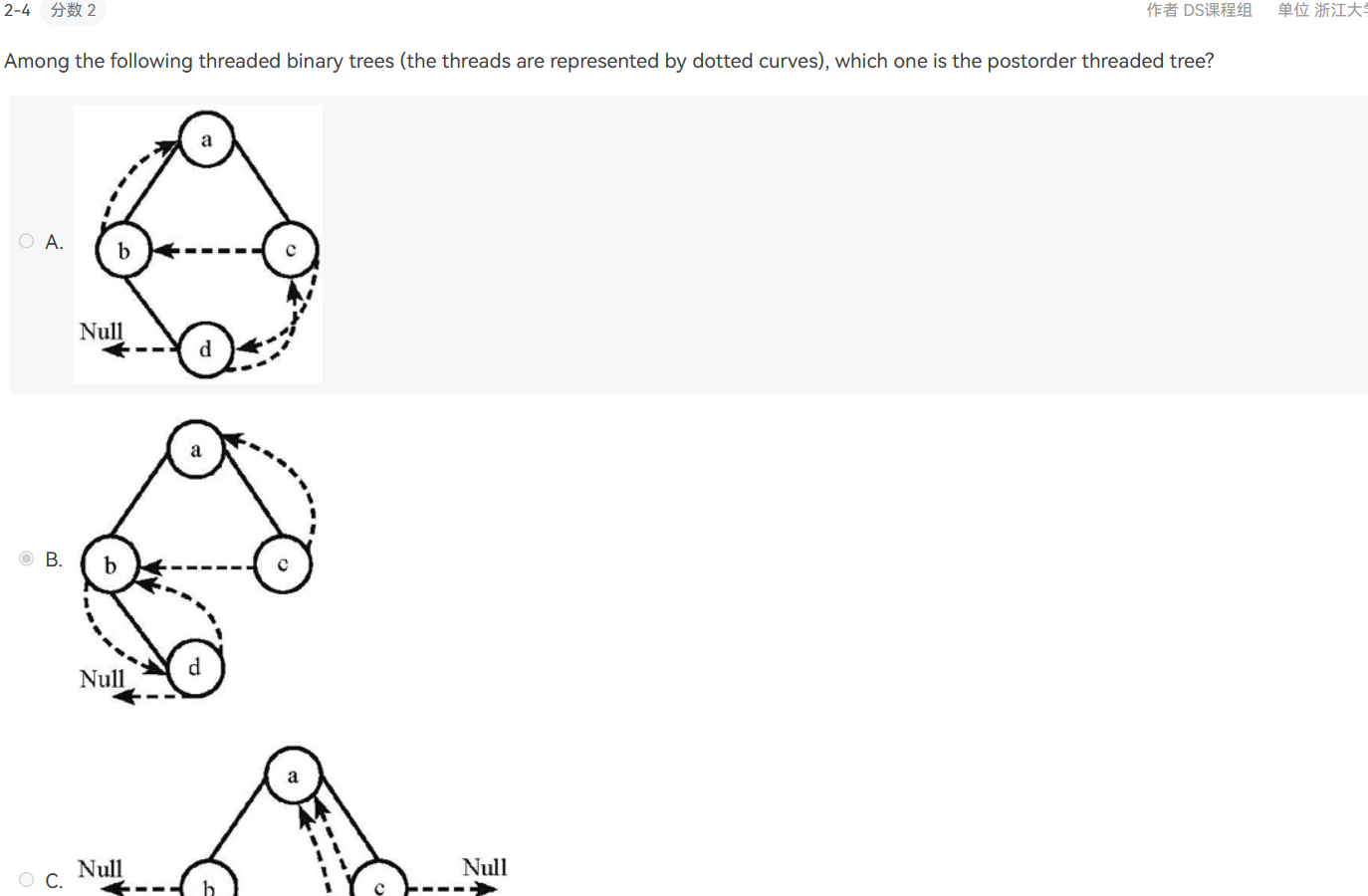
![ex5]()
首先定义添加线索的规则:
若结点的左子树为空,则该结点的左孩子指针指向其前驱结点;若结点的右子树为空,则该结点的右孩子指针指向其后继结点
这种指向前驱和后继的指针称为线索,将一棵普通的二叉树以某种次序遍历,并添加线索的过程称为线索化。
- 填空题1(从任意两种遍历构造二叉树)
hint:可以考虑在递归时对函数做手脚(联想数组退化成指针)
堆(chapter 5)
堆的具体知识点
堆是一种非线性数据结构,可以被看做是完全二叉树(comlplete tree)。它有一个或多个有序的子序列,各子序列又是一个堆。通常,堆可以分为两种类型:最大堆和最小堆。
从根节点出发到任意节点是有序的
最大堆:在最大堆中,父节点的值总是大于或等于其子节点的值。此外,每个子树也都满足这个条件。也就是说,最大堆的最大元素,即根元素,总是位于顶部。
最小堆:在最小堆中,父节点的值总是小于或等于其子节点的值,并且每个子树也都满足这个条件。也就是说,最小堆的最小元素,即根元素,总是位于顶部。
堆有以下一些基本特性和操作:
结构性:堆的结构一般总是一个完全二叉树,这样可以有效地利用数组存储堆的元素,并通过索引迅速定位一个节点的父节点或子节点。
插入元素:唯一可插点为最后一个元素,在堆中插入元素后,可能需要恢复堆的特性,这个过程称为“堆化(heapify)”。这通常可通过一种称为“上浮(percolate up)”或者“下沉(percolate down)”的操作来完成。
$T(N)=O(log N)$删除元素:一般我们总是删除堆顶元素,也就是最大或最小元素。然后将堆的最后一个元素移动到堆顶,然后进行下沉操作,恢复堆的特性。
example
1 | |
$T(N)=log N$
- 建堆:给定一个未排序的数组,可以通过多次进行下沉操作来生成一个新堆,这个过程叫“建堆”。(从右下到上每次对一个小堆进行下沉操作)
堆的主要应用场景包括堆排序以及优先队列。例如,操作系统中的任务调度、Dijkstra 算法中的优先队列等都可能用到堆。
- 一个个插入$T=O(NlogN)$
- 直接将这个序列看作完全二叉树,从最后一个非叶节点开始进行percolatedown,复杂度$T=O(N)$
- 大小顶堆的转化(与建堆思路类似)是线性算法
堆的题目
- ex1
![ex1]()
这个题目是对最大堆中可能的最小元素的下标的探讨,对于完全的堆则存在:$1+2+2^2……$即$2^t-1$,而最后一层若满则是$2^t$,且[n/2]为其父节点的下标,则尽可能为[n/2]+2
- ex2
![ex2]()
note:非叶节点不可能是最大元素,当然最坏的情况为O(N)
并查集(chapter 8)
并查集的具体知识点
并查集是一种数据结构,它包含多个不相交的集合,每个集合由一个代表元素(通常称为“根”)表示。并查集支持两种基本操作 :“find”和“union”。
- find操作用于查找元素所属的集合,也就是查找元素的根元素。
- union操作用于将两个集合合并为一个。
两种优化方式
- union by size
Union by Size是指在进行union操作时,我们总是将元素数量较小的集合(树)附加到元素数量较大的集合(树)上。这是基于一个思路:将小树添加到大树的高度不会增加。因此,这种方法有助于保持树的高度较小,从而使查找操作尽可能快。
在实践中,我们往往通过让每个集合(或树)的根节点存储其所在集合的元素数量(或称为“大小”),以便进行“union by size”。
而在具体的实践中,我们需要记住每一棵树的大小,因此可以让每一个根的数组元素包含它的树的大小的负值,其余则要求一样。
注:并且若union都是按照大小进行,则任何节点深度均不会超过logn - union by height
我们总是将较矮的树附加到较高的树上。与“union by size”类似,这是为了尽可能地保持树的高度小。
压缩路径
在查找的同时将路径上的所有节点的父节点都设置为根节点,这样可以减少树的高度
1 | |
题目
- ex1
![ex1]()
首先是知道负数肯定代表是根节点,然后将逻辑图画出,并遵循小树加到大树的规则
图(chapter 9)
图的定义(9-1)
- G(V,E):G为图,V为顶点,E为边
- undirected graph:(vi,vj)=(vj,vi)
- directed graph:有tail和head (vi is adjacent to vj)
- restriction:self loop is forbidden;mutigraph is not considered
- complete graph(具有最大边):
无向图:边数n(n-1)/2;有向图:边数n(n-1) - 路径
- 路径的长度(路径上的边数)
- simple path(顶点均不相同)
- 若无向图connected(则每一组不同的顶点存在路径)
- component of an undirected graph(最大的联通子图)
- tree(一个连通图但是acyclic(无环))
- DAG(a directed acyclic graph)
- strongly connected directed graph G(对于每一个顶点vi,vj,都存在着vi到vj和vj到vi的分量)
- strongly connected component(最大强连通子图)
- weakly connected:有向图的底图(无向图)是连通图,则称为弱连通
- degree(对于有向图则是出度和入度) (入度指向该顶点)
- $e=(\sum_{i=1}^{n}d_i)/2$ 其中e为边数,$d_i$为$v_i$的度数
- 欧拉公式:r=e-v+2
图的表示(9-2)
adjacency martrix
adjacency list(replace each row by a linked list)
- 如果图是无向的,degree[i]就是graph[i]中的节点数 T(exam)=O(n+e)
- 如果图是有向的,只考虑入度即可(Add inverse adjacency list 逆邻接表)
adjacency multilist
其中,顶点表由两个域组成,vertex 域存储和该顶点相关的信息firstedge 域指示第一条依附于该顶点的边;边表结点由六个域
组成,mark 为标记域,可用以标记该条边是否被搜索过;ivex 和jvex 为该边依附的两个顶点在图中的位置;ilink 指向下一条依
附于顶点ivex的边;jlink 指向下一条依附于顶点jvex 的边,info 为指向和边相关的各种信息的指针域。
拓扑排序(9-3)
- AOV network(顶点代表活动,边代表先后关系)
- i is a predecessor(前任)of j:有一条路径从i到j
- i is an immediate predeccessor of j:<i,j>属于E(G),j叫做i的successor
- partial order:a precedence relation which is transitive and irreflexive
- topological sort:如果i是j的前任那么在这个ording中i在j的前面(可能并不唯一)
- 具体实现:根据入度进行实现(将入度为零的压入栈中,每次操作其后的节点入度减一)
最短路径(9-4)
single source shortest——path problem(给定图,找到一个固定顶点到其他顶点的最短路径)
- unweighted path(宽度优先搜索BFS)
具体实现方法(用三个数组进行存储Dist存储该节点到给定节点的距离;Konwn存储是否该节点已经被访问;Path追踪路径)
具体实现代码时的改进措施(利用堆栈进行改进)
开始将源点压入栈中,进入循环(循环的判定标准是栈是否为空):每一次都将一顶点1从栈中弹出,然后访问该顶点1的邻顶点2。如果其distance为infinity,则其distance为当前的顶点1的distance加1,并将邻顶点2压入栈中。此时的算法T=O(V+E)
- dijkstra algorithm(解决有权值的图)
- S为集合,其中的各个顶点到原顶点的最短路径已经知晓,那么对于还不在S中的顶点u,$distance[u]=min(path s=>vi=>u)$
- 对于带负权值的图不起作用
- implementation1:V是最小距离的未访问的顶点(需要对图扫描) $T=O(V^2+E)$ 如果图稠密比较好
- implementation2:利用一个优先数列即堆来keep distances
method1(decreasekey-o(logV)):$T=O(VlogV+ElogV)=O(ElogV)$
method2(将w插入优先队列):$T=O(ElogV)$
- 带有负值的图
采用类似于unweighted时的算法,利用一个堆栈进行处理,只是在中间的处理过程中使用$T[v].dist+cvw与T[w].dist$进行比较,$T=O(V*E)$
- acyclic graphs(知识点不清晰)
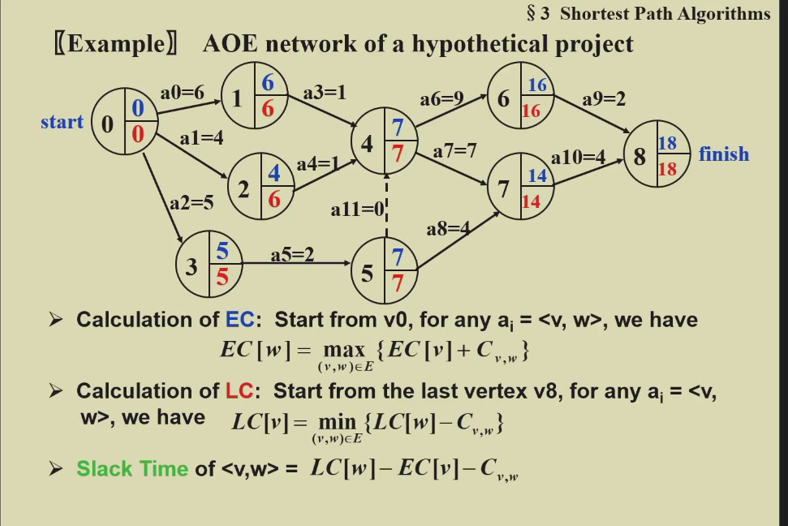
![acyclic]()
定义:
- 最早完成时间(earliest completion time)
EC:start from v0,for any $a_{i}=<v,w>$,EC[w]=max{$EC[v]+C_{v,w}$} - 最晚完成时间(latest completion time)
LC:start from v8,for any $a_{i}=<v,w>$,LC[w]=min{$LC[W]-C_{v,w}$} - slack time of $<v,w>=LC[w]-EC[v]-C_{v,w}$
all-pairs shortest path problem
use single-source algoritms for V times
$T=O(V^3)$-works fast on sprase graph
网络流(9-5)
网络流的基本性质
Total coming in (v)恒等于 Total going out(v),并且v不是起始点也不是终止点
我们研究问题的核心是是找到从s到t的最大流
a simple algorithm
准备三张图 G Gr Gf
首先在Gr中对于任意一条从s到t的路径
将这个路径中的最短边看作流的大小,并将路径加到Gf上面
更新Gr,将边为0的删除掉
如果Gr中还存在路径重复上述操作
note:这种方法可能存在一些问题:在例子中我选择了一条路径,进行在Gr上的更新之后发现已经不存在通路了
a solution-allow the algorithn to undo its decisions
- 每次找到Gr的一条路径时添加一条反向的流在Gr中并重复之前的操作,知道Gr中没有从s到t的路径。
- 注:如果边的容量是有理数(rational numbers),那么该算法在终止时总能得到一个最大流
analyse(在前提边是整数的情况下)
我们可以通过无权最短路径算法找到augumenting path(增广路径)
时间复杂度$T=O(f⋅∣E∣)$,f表示最大流量
但是存在一种特殊情况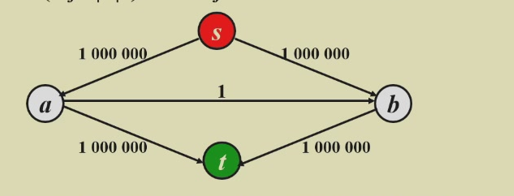
有两种解决办法
在选择增广路径时,总是挑选对流量提升最大的路径(djkstra的变式)$T=T_{augumentation}+T_{find a path}=O(Elog cap_{max}*Elog(V)=O(E^2log(V)))$
选择具有最短边的增广路径
$T=T_{augumentation}+T_{find a path}=O(E^2V)$
others
对于某些特殊情况,时间复杂度还可以降低:如果除了源点和汇点外的所有顶点的入边容量为1,或者出边容量为1,那么最优算法的时间复杂度为
$T=O(Ev^{1/2})$
minimum spanning tree(9-6)
definition of it
- spanning tree:包含所有顶点的一颗树
- minmum spanning tree:
- acyclic 并且number of edge is V-1
- 边的权重最小(总权重一定唯一)
- 包含所有顶点
- 图是联通时最小生成树存在
- 增加一条边形成一个环
plim algorithm(与dijkstra十分相似)
分为两个集合,其中a类最初只有起始点,然后开始找a的邻居与a的边,找出最小值将对应的邻居放进a中;再重复操作,寻找a类里面所有顶点的还在b中的邻居,找出最小值,直到b中元素即可
kruskal algorithm
- 初始情况下有V棵树
- 然后通过添加一条最短的边,合并两棵树(可以采用并查集的原理),如果该边对应的两点已经在一个集合里则不需要添加进去。
- 也可以用堆进行维护
application of depth-first search(类前序遍历)(9-7)
基础原码实现
1 | |
- 当且仅当一次DFS遍历所有顶点时,无向图是连通的
- 可以用深度优先生成树形象的展示DFS的过程
1 | |
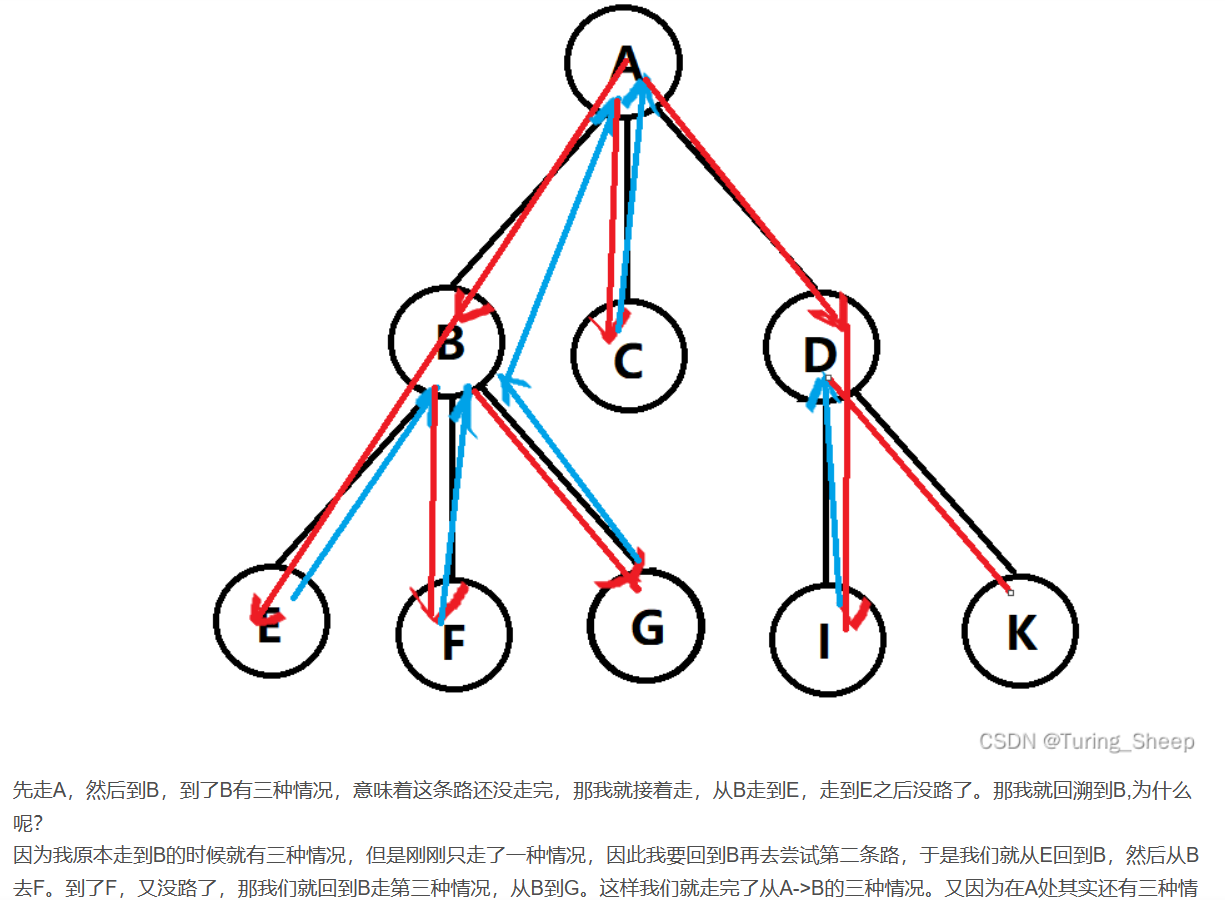
biconnectivity(双连通性)
- v is an artigulation point if $G^{‘}=Deletevertex(G,v)$ 至少有两个连通分量(去掉该点影响连通性)
- G is a biconnective graph 如果G是连通的并且,G没有artigulation point
- bioconnective component 是极大双连通子图(无法再添加节点使之保持双连通性)
- 理解:在无向图中,一个图称之为双连通的,意味着该图中任意两个顶点之间至少存在两条完全不同的路径,即使去掉图中的任意一个顶点(和与之相连的边),图仍然是连通的。换句话说,没有一个顶点会导致图的分裂。
- 寻找无向连通图中的所有双连通分量
![]()
- 两个条件找关节点(割点)
- 进行割点计算的DFS,在找到一个割点的时候已经完成了一次对某个极大双连通子图的访问。那么在进行DFS的过程中,把遍历过的点保存起来,就可以得到这个点双连通分量。
- 所使用的变量:num(顶点v的前序遍历编号) low(生成树中顶点v的所有孩子节点以及v回边上的顶点中Num的最小值)
- 当且仅当除根节点外的顶点u至少有1个孩子,且该孩子与它的祖先之间没有回边(即Low(child) >= Num(u))时,u为关节点
![]()
欧拉回路
欧拉路(euler tour):对于一个图,每条边可以且只能访问一次
欧拉回路(euler circuit):在欧拉图的情况下,最后要回到原点。也就是说欧拉路不一定是欧拉回路,但欧拉回路一定是欧拉路
性质:
若图 G 不存在度为奇数的端点时,则图 G 有欧拉回路,即无向连通多重图中存在欧拉回路当且仅当图中所有顶点的度数为偶数
若图 G 存在且仅存在 2 个度为奇数的端点时,则图 G 有欧拉通路,其起点为其中 1 个度为奇数的端点,终点为另一个度为奇数的端点,即在无向连通多重图中存在欧拉通路且不存在欧拉回路当且仅当连通图中有且只用两个顶点的度数为奇数
若图 G 所有节点的入度等于出度,则图 G 有欧拉回路,即有向连通多重图中存在欧拉回路当且仅当图中所有顶点的入度数等于出度数
若图 G 存在且仅存在 2 个节点的入度不等于出度,且一个节点入度比出度大 1 ,一个入度比出度小 1 ,则图 G 有欧拉通路,其起点为入度比出度小 1 的节点,终点为节点入度比出度大 1 节点,即有向连通多重图中存在欧拉通路且不存在欧拉回路当且仅当连通图中有且只用两个顶点的入度不等于出度,且一个节点入度比出度大 1 ,另一个入度比出度小
例题
- ex1
![oula]()
note:因为要注意题干条件存在cycle,即必须满足所有节点的入度等于出度或者不存在度为奇数的端点
- ex2
![dfs]()
note:要注意题干条件是before the end of each recursion进行打印,则printf语句在声明之后而在return之前
- ex3
![bian]()
note:要注意题干条件强调greater其实存在equal
- ex4
![oula]()
note:这道题较为困难,根据欧拉公式,**$r=e-v+2$(其中r是区域的数量),将一个图的一个联通分量看作一个联通图,假如有k个联通分量,求和可以得到,R=E-V+2k。但是注意到所有联通分量中最外部的那个区域被计算了k次,其实只需计算一次,因此需要减掉。$R=E-V+2k-(k-1)=E-V+k+1$**
这就是任意图都能使用的欧拉公式。
代入可得:k=R+69,为了让联通分量最小,取R=1,即k=70
- ex5
![qiangliantong]()
note:这道题就是通过将邻接表转化为图,然后根据强连通组件(隐含max)来进行做题
排序(chapter 6)
排序的稳定性
也就是说在排序前后,两个相等的数相对位置不变,则排序算法是稳定的,如果相对位置发生改变,则排序算法是不稳定的。例如冒泡排序、插入排序、鸡尾酒排序、桶排序、计数排序、归并排序、基数排序等都是稳定排序。快速排序、希尔排序、堆排序、直接选择排序等则是不稳定排序(快希堆直选)。
希尔排序
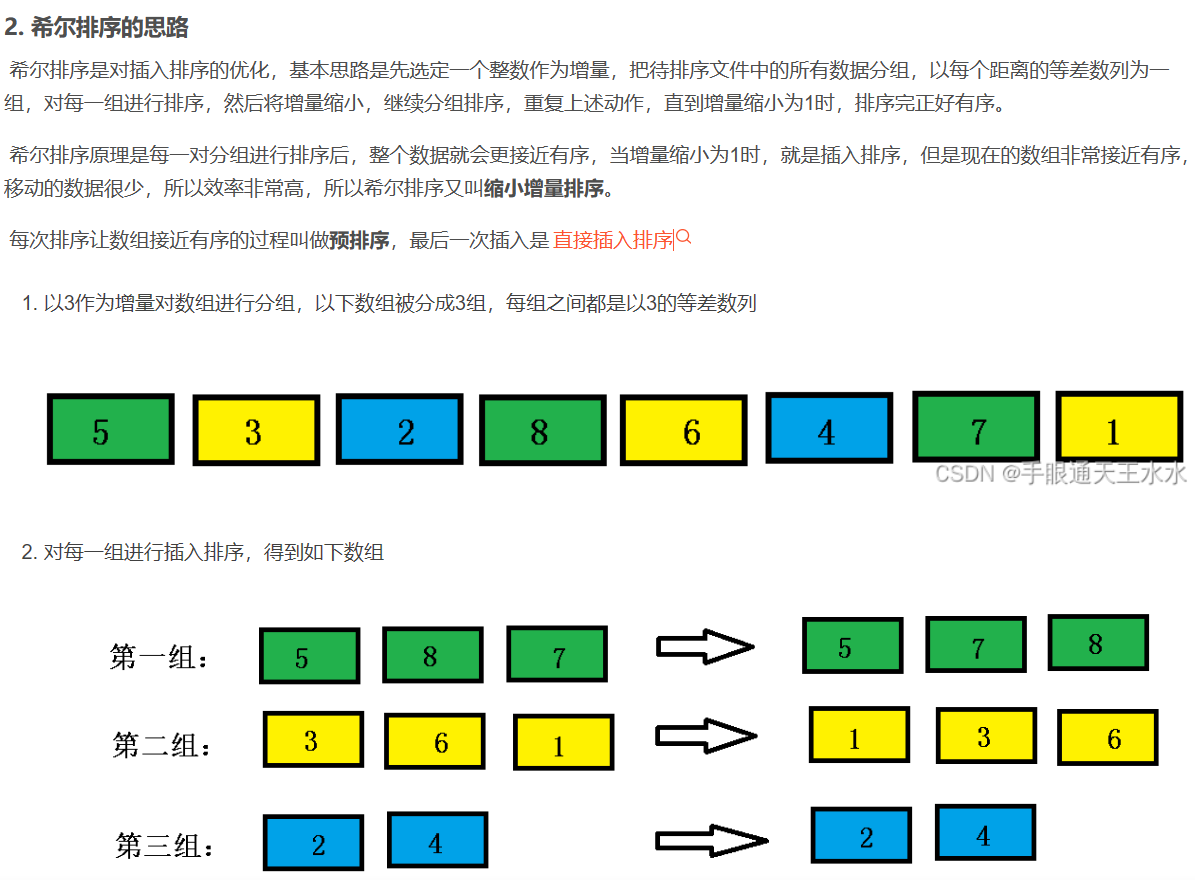
- 此时增量缩小,以2为增量对数组进行分组,数组被分成2份,每组之间都是2的等差数列
对每一组进行插入排序,得到如下数组
最后增量为1,分为1组(其实就等于没分),对其进行插入排序,数组变得有序 - 希尔增量序列:$h_{t}=[N/2],h_{k}=[(h_{k+1})/2]$
- 最坏时间复杂度$O(N^2)$
- 改进:Hibbard 增量序列 $h_{k}=2^k-1$
最坏$O(N^{3/2})$ 平均$O(N^{5/4})$
插入排序
1.从第一个元素开始,该元素可以认为已经被排序
2.取下一个元素tem,从已排序的元素序列从后往前扫描
3.如果该元素大于tem,则将该元素移到下一位
4.重复步骤3,直到找到已排序元素中小于等于tem的元素
5.tem插入到该元素的后面,如果已排序所有元素都大于tem,则将tem插入到下标为0的位置
6.重复步骤2~5
时间复杂度:最坏情况下为O(N*N),此时待排序列为逆序,或者说接近逆序
最好情况下为O(N),此时待排序列为升序,或者说接近升序。
空间复杂度:O(1)
选择排序
时间复杂度永远为O($N^2$)
堆排序
- 建堆
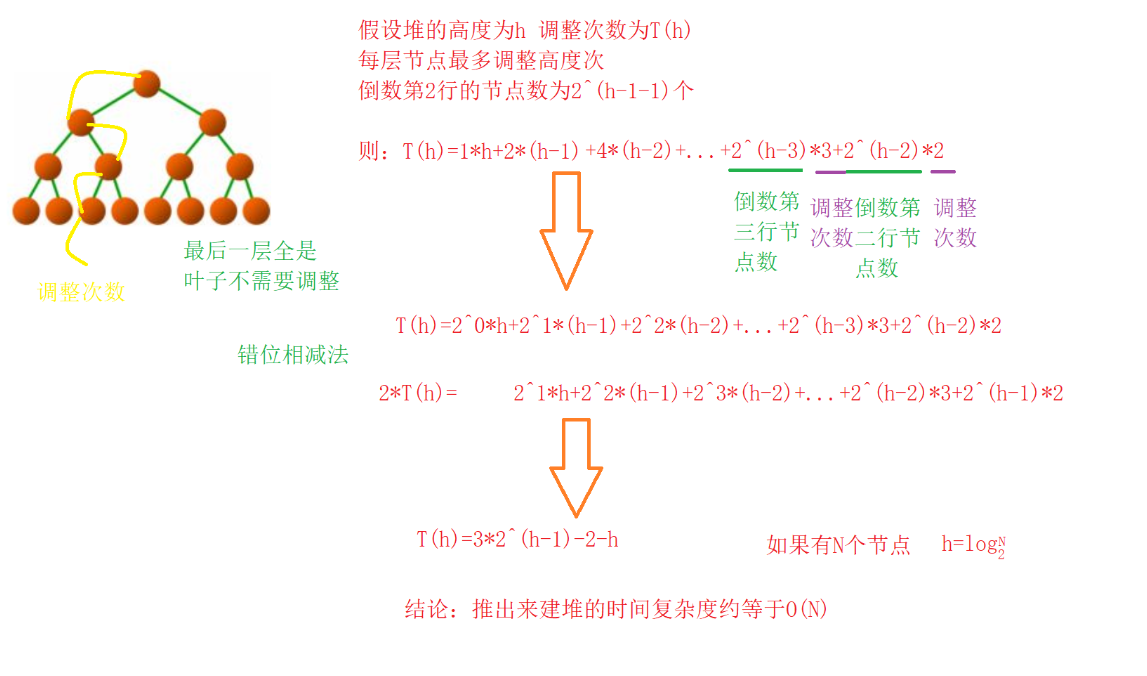
由以上推论过程可得建堆的时间复杂度为O(N);
向下调整算法的时间复杂度为O(log2N);
所以堆排序的时间复杂度为O(N*log2N);
快速排序
pivot事实上可以随机选取
最坏:O($n^2$)
最好: O(nlogn)
平均: O(nlogn)
当n小于20时quick sort slower than insert sort
具体实现方法:
首先选择一个基准值,然后在已知区间中,left向右移动,right向左移动,left在大于基准值时停下,right在小于基准值时停下,做交换。直到两者相遇,将相遇的点与基准值点交换。
桶排序与基数排序(bucket and radix sort)
1 | |
时间复杂度分析:
最好时间复杂度 : O(n + k)
其中k为桶的个数。即当数据是均匀分散排列的,那么每个桶分到的数据个数都是一样的,这个步骤需要O(k)的时间复杂度,在对每个桶进行排序的时候,最好情况下是数据都已经是有序的了,那么最好的排序算法的时间复杂度会是O(n),因此总的时间复杂度是 O(n + k) 。
最坏时间复杂度:O(n^2)
当对每个桶中的数据进行排序的时候,所使用的排序算法,最坏情况下是O($n^2$)
因此总的最坏情况下的时间复杂度为O($n^2$)。
平均时间复杂度:O(n + n²/k + k) <=> O(n)
如果k是根据Θ(n)来获取的,那么平均时间复杂度就是 O(n)。
一些结论
可以证明 T(N)>=k*nlogn
worst case computing time
排序题目
ex1
![ex1]()
ex2
![ex2]()
ex3
![ex3]()
哈希表(chapter 7)
哈希表定义
哈希表,又名做散列表,是根据关键字和值直接进行访问的数据结构。也就是说,它通过关键字 key 和一个映射函数 Hash计算出对应的值hash value,然后把键值对映射到表中一个位置来访问记录,以加快查找的速度
哈希函数
哈希函数示将哈希表中元素的关键键值映射为元素存储位置的函数。一般情况下哈希函数具有一下性质:
哈希函数应该易于计算,并且尽量使计算出来的索引值均匀分布,这能减少哈希冲突
哈希函数计算得到的哈希值是一个固定长度的输出值
如果 Hash(key1) 不等于 Hash(key2),那么 key1、key2 一定不相等
如果 Hash(key1) 等于 Hash(key2),那么 key1、key2 可能相等,也可能不相等(会发生哈希碰撞)
哈希表操作的时间复杂度
搜索:1.无哈希碰撞,直接用哈希函数通过Key定位到内存地址,复杂度O(1)
2.有哈希碰撞,因为存在内存地址需要通过链表查询,复杂度O(N)插入:通过key找到内存地址插入即可,复杂度 O(1)–自动插入
删除:通过key找到内存地址删除即可,复杂度 O(1)
哈希知识补充
负载因子 $\lambda$ = 填进表中的元素个数(n) / 哈希表的长度(b)*槽(s) slot
标识符密度定义$n/T$ T表示标识符x可能的不同值的个数


注意:
如果插入和删除混合,插入会变得十分慢
哈希表解决冲突
无论如何设计散列函数,都无法避免发生冲突。
如果发生冲突,就需要处理冲突。
处理冲突的方法分为4种:
开放地址法
链地址法
二次哈希
重哈希
开放地址法(oprn addressing)
- 线性探测法(linear probing)
线性探测法是最简单的开放地址法,线性探测的增量序列为di =1,…,m -1。
例如,有一组关键字(14,36,42,38,40,15,19,12,51,65,34,25),若表长为15,散列函数为hash(key)=key%13,则可采用线性探测法处理冲突,构造该散列表。
按照关键字顺序,根据散列函数计算散列地址,如果该地址空间为空,则直接放入;如果该地址空间已存储数据,则采用线性探测法处理冲突。
[1] hash(14)=14%13=1,将14放入1号空间(下标为1);hash(36)=36%13=10,将36放入10号空间;hash(42)=42%13=3,将42放入3号空间;hash(38)=38%13=12,将38放入12号空间。
[2] hash(40)=40%13=1,1号空间已存储数据,采用线性探测法处理冲突。
hash′(40)=(hash(40)+di )%m ,di =1,…,m -1
d1 =1:hash′(40)=(1+1)%15=2,2号空间为空,将40放入2号空间,即hash(40)=40%13=1→2。
[3] hash(15)=15%13=2,2号空间已存储数据,发生冲突,采用线性探测法处理冲突。
hash′(15)=(hash(15)+di )%m ,di =1,…,m -1
d1 =1:hash′(15)=(2+1)%15=3,3号空间已存储数据,继续进行线性探测。
d2 =2:hash′(15)=(2+2)%15=4,4号空间为空,将15放入4号空间。

小总结:
线性探测法:$F(i) = 1, 2, 3, …, m - 1$。
二次探测法(quadratic probing):$F(i) = 1^2, -1^2, 2^2, -2^2, …, \pm n^2(n \le m / 2)$。
适用于质数的表
伪随机数序列:$F(i) = 伪随机数序列$。
使用线性探测法:得到下一个地址 H(1) = (5 + 1) % 11 = 6,仍然冲突;继续求出 H(2) = (5 + 2) % 11 = 7,仍然冲突;继续求出 H(3) = (5 + 3) % 11 = 8,8 对应的地址为空,处理冲突过程结束,记录填入哈希表中序号为 8 的位置。
使用二次探测法:得到下一个地址 H(1) = (5 + 11) % 11 = 6,仍然冲突;继续求出 H(2) = (5 - 11) % 11 = 4,4 对应的地址为空,处理冲突过程结束,记录填入哈希表中序号为 4 的位置。
使用伪随机数序列:假设伪随机数为 9,则得到下一个地址 H(1) = (9 + 5) % 11 = 3,3 对应的地址为空,处理冲突过程结束,记录填入哈希表中序号为 3 的位置。
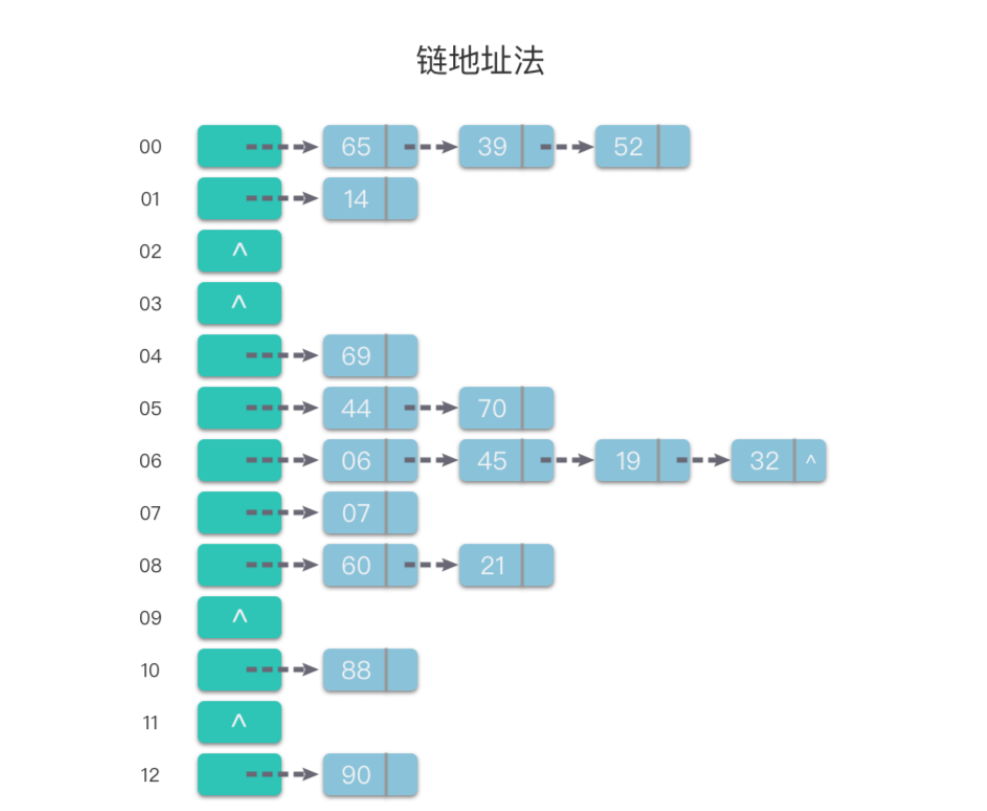
链地址法(separate chaining) 存在问题
假定哈希函数为 Hash(key) = key % 13,哈希表的表长 m = 13
通过链地址法得到的结果如下:
二次哈希法(double hashing)
最后一个是双重hash:
这个很有它的特点,当正常hash时产生了冲突就使用第二个hash函数,形如
hash1(key) = key % TABLE_SIZE
hash2(key) = PRIME – (key % PRIME)
有两个hash的就可以算
第二个hash算出的结果就是待插入元素要从冲突位置往后移的格数,如果往后移了之后还是冲突就继续往后移相同格数,就这样一直移,如果都移过一个循环了,还是没找到可以插入的位置,那就是不能插入了,只能放弃。
重哈希(rehashing)
常常把哈希表开大两倍(此时大小为大于两倍的最小质数),然后再重新插入进行哈希操作
什么时候重哈希:
- 当表格一半满时,
- 当一个插入失败时,
- when the table reaches a certain load factor
哈希例题
ex1
![ex1]()
ex2
![ex2]()
观众老爷能赏口饭吃吗