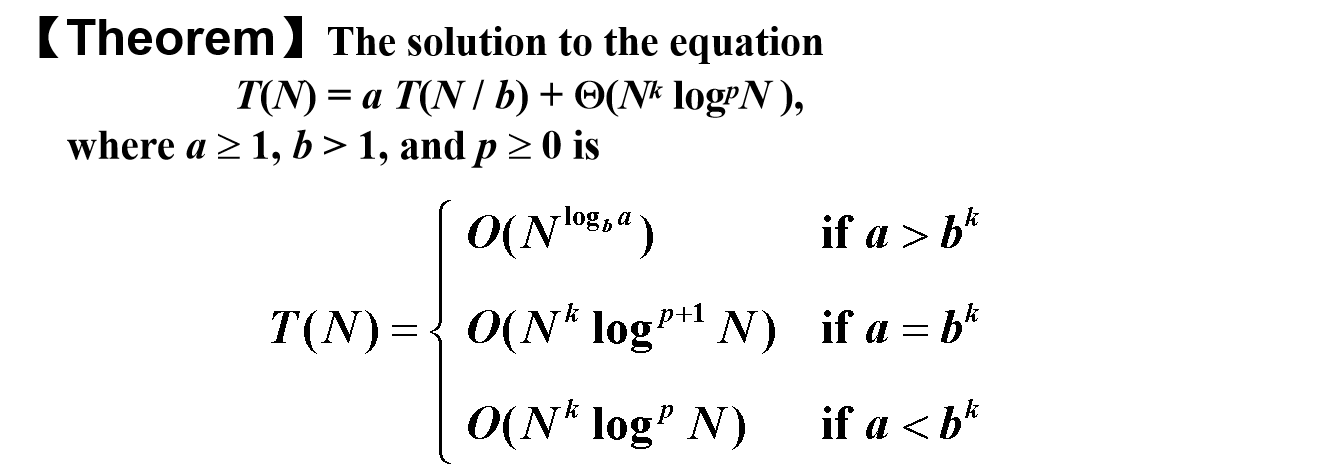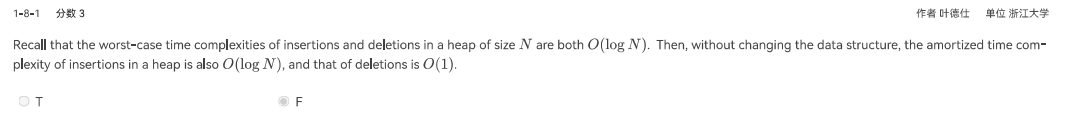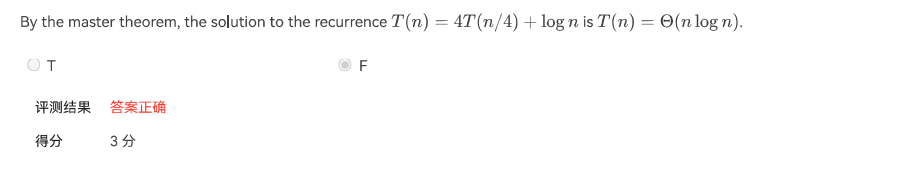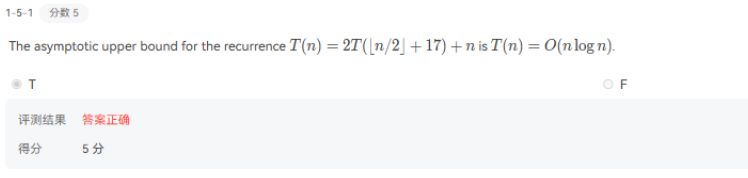ads知识
introduction
lz的排版按照myc老师的教学安排方式,可能里面有一些概念的定义与ppt不同,请以课程ppt为主。
特别鸣谢修佬的ads笔记,我的笔记中的许多图片都来自修佬
hw1 AVL树和红黑树
补充知识:
- avl树中平衡因子的定义:$h_{L}-h_{R}$
- 红黑树中黑高的定义:the number of black nodes on any simple path from the root to a leaf.
- 红黑树中的一个lamma:n个内部节点的红黑树的最大高度为$2ln(n+1)$
知识1 在AVL树中四种样例的划分是来自于 troublemaker、 troublefinder retated child 与 troublefinder
(总结:关注trouble finder(距离案发现场最近的trouble finder)的孩子(trouble finder’s child,left or right)的孩子树(left or right)是否包括troublemaker,例如 LR,表示的是 Trouble Maker 在 Trouble Finder 的 L 孩子节点的 R 孩子树中。)知识2 在AVL中四种样例的具体调整方法还是不太清楚(并且由于对称性,我们综合下来就是两种情况,一种情况进行单次旋转,一种情况进行两次旋转)
知识3 AVL树的节点数量递推式
$n(h)=n(h-1)+n(h-2)+1$知识4 若AVL树进行删除操作只会影响到一个节点,但是当我们修复后矛盾可能往上移动,所以可能需要$Olog(n)$次旋转
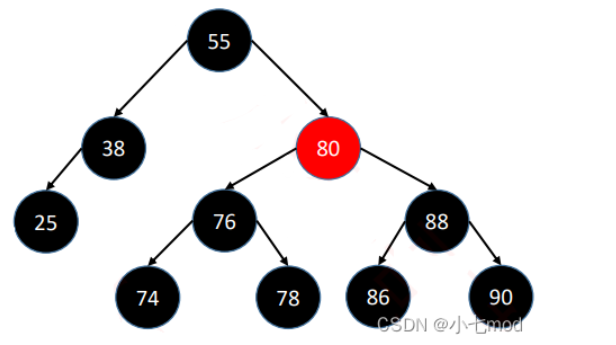
知识5 红黑树的定义
- 每一个节点都是黑色或者红色
- 根一定为黑色
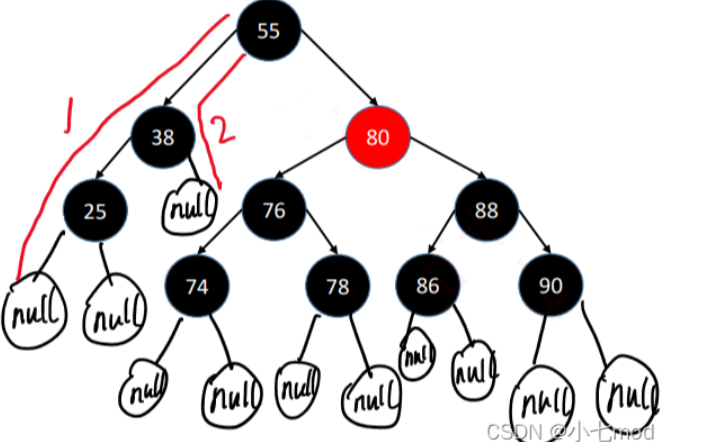
- 叶子(要注意叶子节点一定是空节点,这个概念是很关键的)都为黑色
- 红色节点的孩子一定为黑色
- 对每一个节点,从该节点到叶子的路径中均有数量相同的黑色节点。
![hw1zs1]()
![hw1zs2]()
知识6 红黑树的插入(冲突的三种情况的调整)以及相关的不平衡调整情况
- 先将整个红黑树当作一个普通的二叉搜索树,将目标数据插入到树的末端(也就是置换一个 NIL 节点),并将它染为红色,再调整使之在保证黑高不变的情况下,满足红色节点不能相邻的要求。(因为我们这样操作后,原有的黑高性质不会被破坏,但是可能出现红色节点相邻的情况)
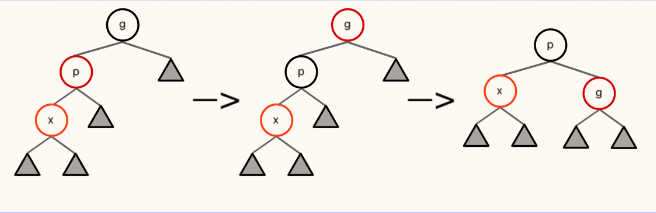
- 此时,插入操作后可能存在下述三种情况:
![hw1zs3]()
(操作为上方红节点染黑及它的父亲染红加旋转)![hw1zs4]()
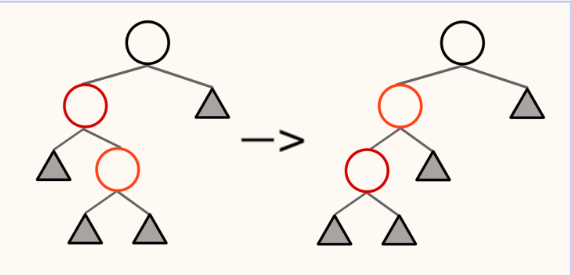
(操作为旋转,转化为上面的样例1)![hw1zs5]()
(操作为染黑这两个红兄弟与染红它们的父亲,矛盾上移,则可能会出现4种情况(其中可能存在这三种情况的相互转化,但是核心都是解决问题并将矛盾上移)) - $T=O(h)$
知识7 红黑树的删除以及相关的平衡调整情况
删除的操作与分类:
- 若没有非NIL节点,直接用NIL节点替代
- 若只有一个非NIL节点,直接用非NIL节点替代
- 有两个非NIL节点,将值与左子树最大值或右子树最小值交换,颜色不换然后删去目标点
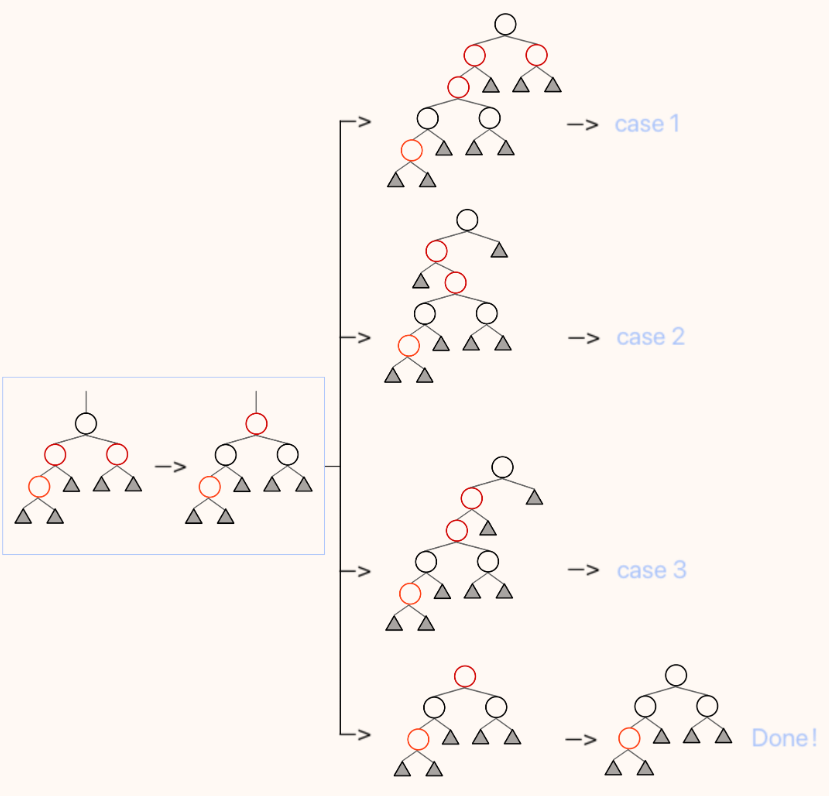
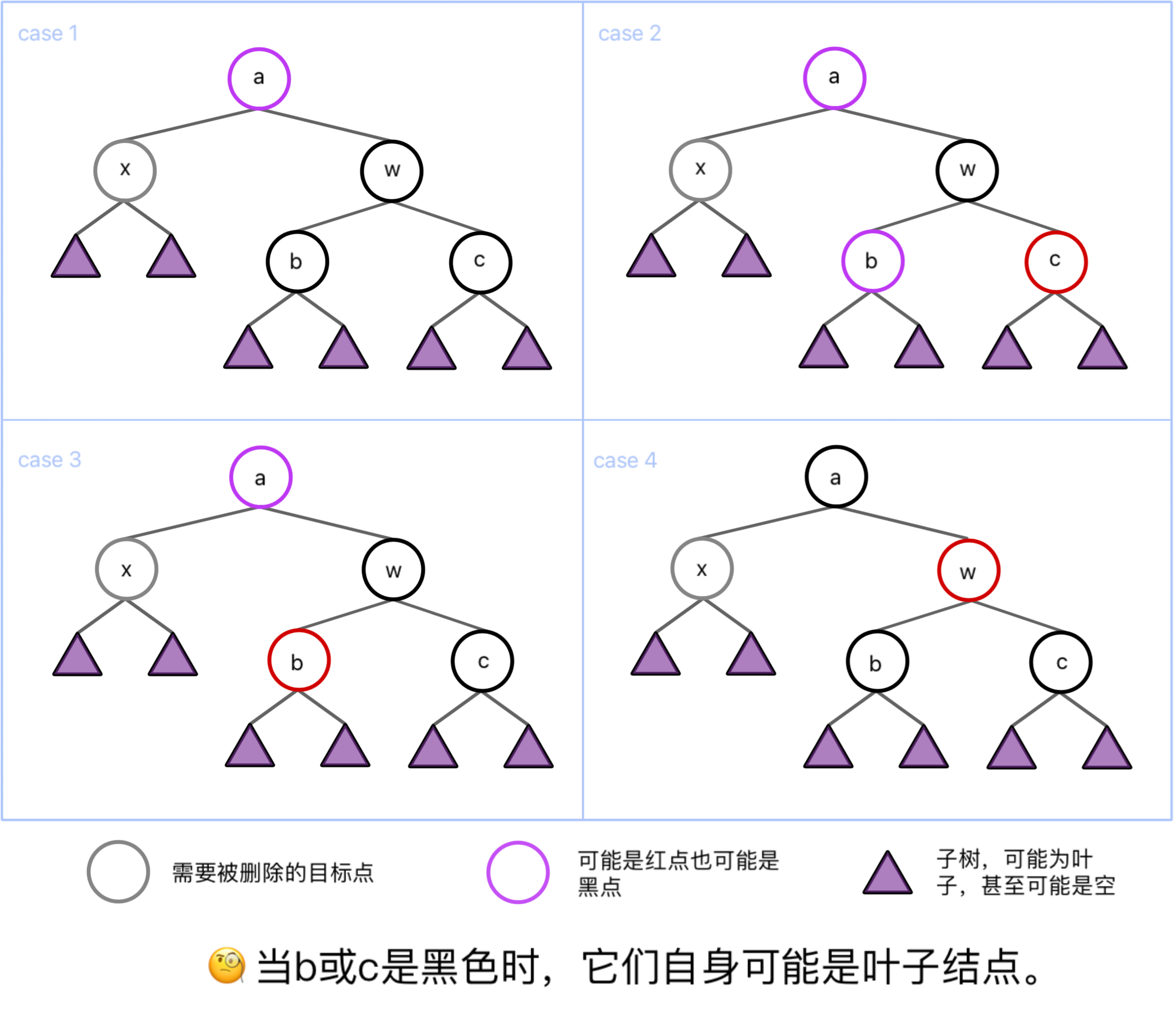
- 如果删除的是红节点不会影响黑高,若删除的是黑节点,我们将红黑树分为以下四类
![hw1zs6]()
删除理解:
- case1(根未知,兄弟和兄弟孩子都是黑):case1.1 若a为红根,则将a和w颜色交换 case1.2 若a为黑根,但是w仍然变化为红色,但是整颗树都标记为灰色(我们可以将这整棵树看作要被删除的X,从而与上方的各个节点的情况综合考虑递归到case1/2/3/4),若此时仍为case1,当a是整颗树的根时我们便可结束操作。
- case2(根未知,兄弟黑,兄弟右孩子红左孩子未知):将w染成a的颜色,再将a和原来红色的儿子染成黑色;再将a左旋
- case3(根未知,兄弟黑,兄弟孩子左孩子红右孩子黑):交换b(红色儿子)和w的颜色;将w右旋转化为case2的情况。
- case4(根黑,兄弟红):交换a和w的颜色,将a左旋,再根据子树a的情况转化为case 1.1/case 2/case 3
删除总结:
旋转的最多情况是case4到case3再到case2即3个,而时间最复杂的情况则是一直递归到整颗树$T=O(logN)$
给一个例子:
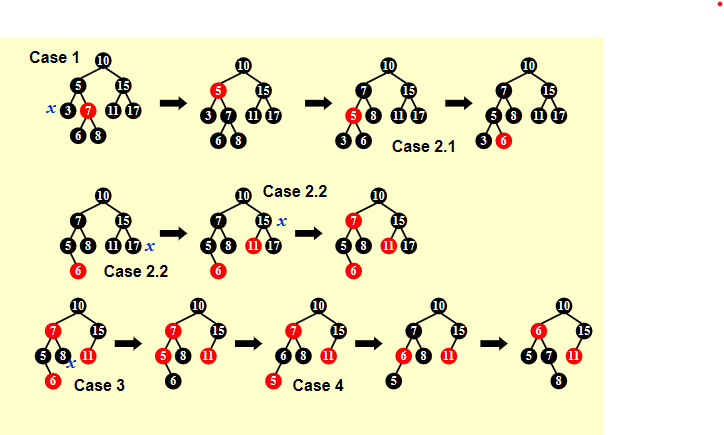
![honghei]()
解释:cy的ppt可能与我参考的修佬的ppt的case有所不同。我们统一称呼待删除的节点为X。对于第一个例子现在是X的兄弟是红的,对应case4:则我们将它们的父亲染红,兄弟染黑并左旋。此时父亲为红,兄弟为黑转化为case1.1:将父亲与兄弟颜色交换,结束操作。
对于第二个例子,父亲兄弟都是黑的,对应case1.2:还是将兄弟染红,将整个子树“染灰”,向上递归观察,发现此时兄弟父亲都是黑色,但是父亲已经是根,根据case1.2,染红兄弟即可。
对于第三个例子,此时我觉得存在镜像,所以应该和我们的case3对应,交换颜色旋转后转到case2,交换兄弟与父亲颜色,父亲与兄弟的红儿子染黑,再旋转,完成操作。ex1:

解释:当对avl树进行删除操作后,则只能有一个点发生不平衡,现在对一这个点为根的子树进行分析。因为我们调整整颗avl树,则首先这颗树的高度会减少1。如果整棵树已经平衡,则停止操作。但是如果因为这颗子树的高度减一导致上方节点的左右子树的高度差大于等于2,则需要上移矛盾再进行操作,则这颗子树的高度可能最终保持不变。
- ex2:
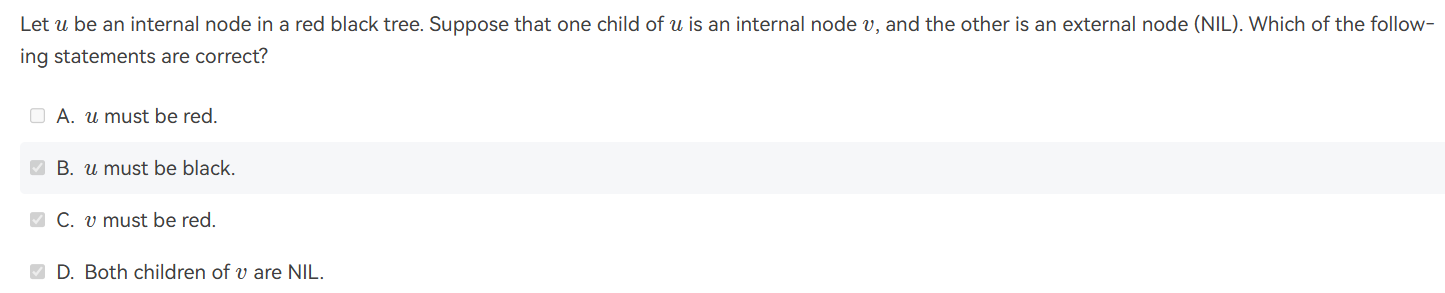
解释:这道题需要结合红黑树的几个基本性质进行解决,u是红黑树的内部节点,其中u有两个孩子,其中一个孩子v是红黑树的内部节点,另一个孩子是nil节点。由红黑树的第五个定义,因为另外一个节点为内部节点则一定有两个nil,由第五个性质,则v一定为红色,再由第四个性质,u一定为黑色。
hw2 摊还分析与splay树
知识1 splay树的具体操作还得记一记喵
- splay树的操作相当简单,首先按照bst进行操作,然后每一次对于操作的节点都进行旋转直到转到根节点处。
- 注意删除时,是先找到节点,然后不断旋转X至根,接下来删除root节点。并在维护BST性质的情况下递归地合并左右子树(splay(左子树最大),attach右子树to左子树);在ppt中说当我们删除X后,此时会出现左右两个子树,我们FindMax(Tl),Make Tr the right child of the root of Tl。
- note:今日又继续做题发现了splay树的操作,自己之前似乎所有情况都按照单旋来考虑,是否是我们的操作要优先考虑双旋转?(期中考试包括期中考试模拟以及第一次期末的历年卷都出现了这个问题)
3.1 之前我对于splay树的旋转一直是采取avl的旋转规则,当然这是错误的
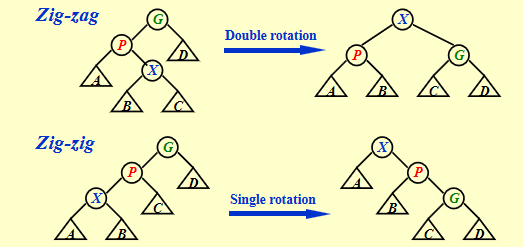
3.2 对于splay树的旋转一共只有两个case:
case1:我们的目标点为X,其父亲为P,如果P是根我们单旋转X到根即可
case2:此时分为zig-zag和zig-zig两种情况,一定要注意zig-zig的情况的操作与AVL树中的LL情况的操作做区分
![splay]()
知识2 对摊还分析的思考(常用的是势能法)
这里ppt有一个不等式:$worst-case \gt amortized \gt average-case$(因为摊还分析我们不考虑不同操作的可能性)
接下来,我们需要设计一个势能函数
Φ(x),并且根据我们提到过的势能分析法的特性,
Φ(x) 应该具有这么几个特征:
开销大的操作应当倾向让势能降,开销小的操作应当倾向让势能升;
势能高倾向于让某些操作开销大,势能低倾向于让某些操作开销小;
Φ(final)>Φ(initial);知识3 均摊O(logn)
- $\Phi(T)=\sum_{i \in T}log S(i)$,S(i)是第i个节点的后代数量(包括i本身)
- 然后对于splay树的操作,我们的所有操作都基于旋转即,zig,zig-zag,zig-zig最终利用均摊时间的计算公式我们可以证明,$\hat{c_i} \le 1+3(R_2(x)-R_1(x))$
ex1

解释:这是splay树的一个特殊情况,也是最坏情况。当我们将一个递增的序列添加到一个空树中的时候,
每次都是最大值在根节点,所以添加的新的节点在它的右侧,旋转到根节点,均会退化为链表。
- ex2

解释:这道题感觉比较有迷惑性,因为如果这颗树要找某个键值的节点,最多就是O(h)的时间复杂度
而我们根据摊还分析可以证明高度为O(logn),而后每次寻找都在根节点即为O(1),所以综上,时间复杂度为O(m+logn)
- ex3

解释:这是一道均摊分析的题目,所谓摊还分析就是对于任何情况下的操作$cost=actual cost+\Delta \phi=O(target)$,因为题干要求amortized cost为O(1),不妨定义$\phi=the opposite of the number of available cells in the array$,则当普通的添加操作一定符合O(1),研究扩展space时的操作$cost=c+nc+-nc=c$符合O(1),经验证其他选项都不满足条件。
- ex4
![hw24]()
解释:这道题存在疑问(我觉得是perform insertion consecutively?的问题)
hw3 b+tree and heap
补充知识:
- b+tree:T(M,N)(insert)=O((M/log M)log N);Depth(M,N)=$O(log_{[M/2]}N)$;$T_{Find}(M,N)=O(log N)$
- NPl:The null path length.Npl(X) = min { Npl(C) + 1 for all C as children of X }
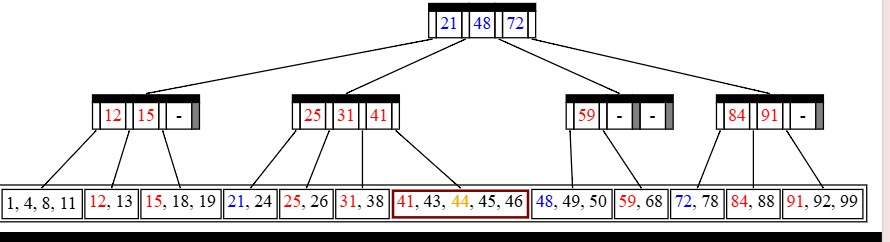
知识1 b+树的定义与性质
![hw3zs1]()
- 根是叶子或者有2到M个孩子
- 所有非叶子的节点(除了根以外),有[M/2]到M个孩子,其本身最多存M-1个值
- 所有的叶子的深度是一样的(真实数据都存储在叶子中)
- 在空间最浪费的情况下是一颗[M/2]叉树,the deep of it is $O(log_{[M/2]}N)$
知识2 b+树的操作
- 查找:类似于不断比较,根据非叶节点的信息找到对应的叶子,然后从叶子中查找。
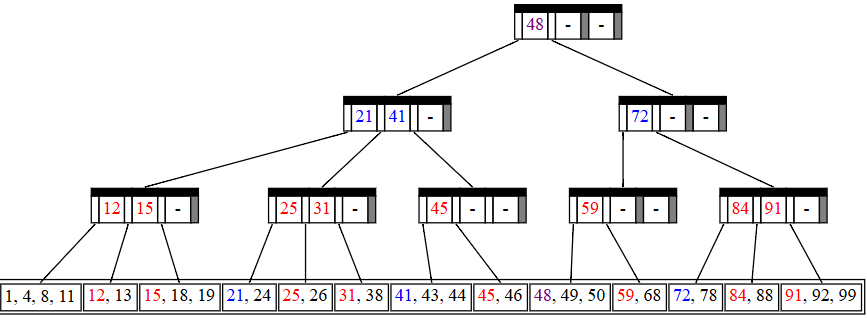
- 插入:首先用与查找相同的方式找到应该插入的位置,然后插入。但是有可能导致叶子节点的数量超过M,此时需要分裂。而分裂会导致家长节点的家长节点的子节点变多,矛盾可能上移。
![hw3zs2]()
![hw3zs3]()
- 删除:首先和查找一样找到待删除的点。直接删除后可能不会直接导致下溢的产生。若可以向兄弟节点(通常先向右兄弟借键)借键,如果兄弟都不足以把键借出,则进行合并操作,并更新父节点。然后就进行非叶节点即索引的判断,如果索引关键字数量不满足且有兄弟节点可借(父节点下移到这个索引中,兄弟节点上移),否则父节点下移合并成新的索引。
知识3 左偏堆(lefttist heap)的定义
- dist in leftist heap:如果一个结点的左孩子或右孩子为空结点则其dist为零,称为外结点。否则$dist=min(dist_{left child},dist_{right child})+1$
- leftist heap:左偏堆是满足结点的左孩子的dist不小于右孩子的dist的堆(这个定义与合并时有关)
知识4 左偏堆的操作
- 合并(核心操作):先维护堆的性质,在回溯时维护左偏性质。(实际上是一个自上而下再自下而上的过程)具体操作,先比较当前两个待合并子树的根结点的键值,选择较小(较大)的那个作为根结点,其左子树依然为左子树,右子树更新为「右子树和另一个待合并子树的合并结果」。当然,在递归地更新完后,我们需要检查左子树和右子树是否满足$dist_{left child}>=dist_{right child}$,如果不满足则交换左右子树。
- 单点插入:本质上就是可以看作合并只有一个结点的左偏堆
- 单点删除:合并需要被删除的结点的两个子结点,将这个新的树的根代替被删除的结点,然后再回溯更新dist调整即可。$O(logn)$
知识5 一个lamma
For a leftist heap with n nodes,its right path from the root to null has most $log_{2}(n+1)$ nodes知识6 斜堆(skew heap)的操作
- 斜堆也需要满足大根堆(小根堆)的性质,而它的合并和左偏堆的合并也十分类似,只不过我们这次无条件的交换左右子树,换句话来说,不管左偏性质如何变化,我们都会选择交换参与合并的左右子树,这样我们就不需要在回溯的时候才进行左右子树的交换,于是就实现了完全的自上而下。
- 非递归实现:把每个堆的每棵(递归意义下)最右子树切下 来。这使得得到的每棵树的右子树均为空。
按root的键值的升序排列这些树。
迭代合并具有最大root键值的两棵树:
具有次大root键值的树的右子树必定为空。把其左子树与右子树交换。现在该树的左子树为空。具有最大root键值的树作为具有次大root键值树的左子树。
知识7 摊还分析skew heap
- $\Phi(Heap)=number of heavy node in Heap$
- 对于一个子堆H,如果$size(H.right_descendant)>=\frac{1}{2}size(H)$则H为heavy node,否则为light node
- 如果一个节点是 heavy node,并且在其右子树发生了合并(包括翻转),那么它一定变为一个 light node;如果一个节点是 light node,并且在其右子树发生了合并(包括翻转),那么它可能变为一个 heavy node;合并过程中,如果一个节点的 heavy/light 发生变化,那么它原先一定在堆的最右侧路径上;
- $c^{1}=c+\phi(H_{merged})-\phi(H_{x})-\phi(H_{y})$,记录$l_{x}为H_{x}最右侧的light node的数量,h_{x}为最右侧heavy node数量,h_{x}^{0}为H_{x}所有不在最右侧路
径上的heavy node数量$,我们可以得到$c=l_{x}+h_{x}+l_{y}+h_{y},\phi(H_{merged})<=h_{x}^{0}+h_{y}^{0}+l_{x}+l_{y}$
$c^{1}<=l_{x}+h_{x}+l_{y}+h_{y}+l_{x}+l_{y}+h_{x}^{0}+h_{y}^{0}-h_{x}-h_{x}^{0}-h_{y}-h_{y}^{0}=2(l_{x}+l_{y})$,而用归纳法可以证明light node的数量的数量级为log。
最后可以得到为$O(logN)$
知识8 ppt中存在的代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19PriorityQueue Merge(PriorityQueue H1,PrioorityQueue H2)
{
if(H1==NULL) return H2;
if(H2==NULL) return H1;
if(H1->Element<H2->Element) return Merge1(H1,H2);//以前面的树的根为根,H2和H1的右子树合并成为新树的右子树
else return Merge1(H2,H1);
}
static PriorityQueue Merge1(PriorityQueue H1,PrioorityQueue H2)
{
if(H1->Left==NULL)
H1->Left=H2;
else{
H1->Right=Merge(H1->Right,H2);
if(H1->Left->NPL<H1->Right->NPL)
SwapChildren(H1);
H1->NPL=H1->Right->NPL+1;
}
return H1;
}从二叉堆的结构说起,它是一棵二叉树,并且是完全二叉树,每个结点中存有一个元素(或者说,有个权值)。
零距离(英文名NPL,即Null Path Length)则是从一个节点到一个”最近的不满节点”的路径长度。不满节点是指该该节点的左右孩子至少有有一个为NULL。叶节点的NPL为0,NULL节点的NPL为-1,也就是我们前文定义的dist
ex1
![hw3ex1]()
解释:现在我们考虑b+树中的插入操作,因为题目的前提条件是leaf node没有发生分裂,则不需要更新internal node中的key。
- ex2
![hw3ex2]()
解释:(我觉得这个问题主要在于我的目光局限于2-3B+树)因为没有underflow操作。期中再编:因为没有发生underflow操作,
hw4 倒序查找与二向堆
倒排索引
倒排索引(inverted file index)是一种常见的文本检索技术,用于快速查找包含特定单词或短语的文档。它通过将单词或短语作为关键字,并将它们出现在文档中的位置记录在一个索引中,从而支持快速的文本检索
知识1 relevance
- 解释:主要是一些概念的明晰。 relevant irrelevant
retrieved(检索) RR IR
not retrieved RN IN
precision=RR/(RR+IR)(针对检索到的文档的精确性)
recall=RR/(RR+RN)(针对相关文档的能否检索的能力) - relevance(相关性) measurement:a benchmark document of collection,a benchmark suite of queries,a binary assessment(二元评估) of either Relevant or Irrelevant for each query-doc pair
- 解释:主要是一些概念的明晰。 relevant irrelevant
知识2 thresholding(阈值)
我们只对最上面的一些重要文件进行检索,通过阈值的设置达到这一个目的。
注意document分布和query分布的评判标准- document:只检索前面x个按权重排序的文档
1.1 对于布尔查询无效
1.2 会遗漏一些重要的文档,因为有截断 - query:把带查询的terms按照出现的频率升序排序
![thre]()
- document:只检索前面x个按权重排序的文档
知识3 分布式索引与动态索引
- distributed indexing(分布式索引)中,each node contains index of a subset of collection
- 动态索引,docs come in over time,docs get deleted。用一个辅助index来存储新的文件,并生成自己的一个positing list,等文件读完了再与main index合并。
- compression(减小posting list存储空间):首先去掉stoping word;然后所有词连成长串存储每个单词的首字母地址。
知识4 measurement
主要研究我们的搜索引擎判断标准评判标准(fast index,fast search,query language),注意区分data(response time,index space)和information(how relevant)的检索![id]()
知识5 vocabulary scanner&vinsertor
- serach trees(通常用B树)
- 哈希的速度更快,但是但是range searches are expensive
知识6 改进
首先是在文档中频繁出现的停用词(stop words),我们并不需要将它们记录下来;其次使用word stemming,将单词转化为母词根从而来减小倒排索引的规模。
二向队列(binomial queue)
- 知识1 二向队列的定义与性质
- 本质上是一系列二项树的集合
- k阶二项树是两个k-1阶二项树合并(直接令其中一颗树成为另外一颗树的新的child)得到
- 知识2 二向队列的操作
- 首先我们可以利用特征比特向量来理解二向队列的系列操作(1011就可以对应$B_{3}B_{1}B_{0}$)
- 合并:其实合并的结果可以通过前面我们所谓的两个队列的特征比特向量相加来得到。合并的过程也是和二进制加法有异曲同工之妙(即先低位合并,再高位合并),T=O(lgN)
- 查询队首:分别找各棵树的最小值,T=O(lgN)(当然如果我们记忆最小值,并且每个操作都进行更新,那么T=O(1))
- 删除队首:先查询,再删除,再合并(也可以通过特征比特向量的计算提前确认结果)
- 知识3 有关二向队列的一些结论
- A binomial queue of N elements can be built by N successive insertions in O(N) time.
可以用势函数进行证明,定义:$\Phi_i=$#trees after the ith insertion.而我们要利用如下不等式:$c_i+\Phi_i-\Phi_{i-1}=2$再累加进行证明。 - Performing N Inserts on an initially empty binomial queue will take O(N) worst-case time. Hence the average time is constant.
- A binomial queue of N elements can be built by N successive insertions in O(N) time.
hw5 回溯
选填小题
- 样例1 tic-tac-toe 题目
- 一般做这个题的时候就直接把所有空全部填满,然后分别查看人与电脑获胜的情况的数目,记为$W_{computer},W_{Human}$(注意在ppt的显示中,computer用叉表示)
- 定义:the goodness of a position $f(P)=W_{computer}-W_{Human}$
- 所以human尽可能使f(P)小
- 样例2 阿尔法贝塔剪枝问题
- 小知识点:when both techniques are combined. In practice, it limits the searching to only $\sqrt{n}$nodes, where N is the size of the full game tree.
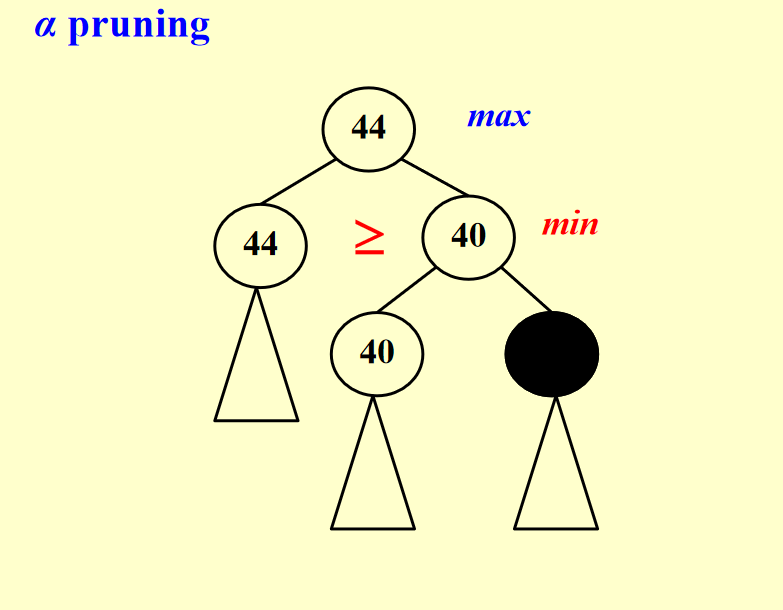
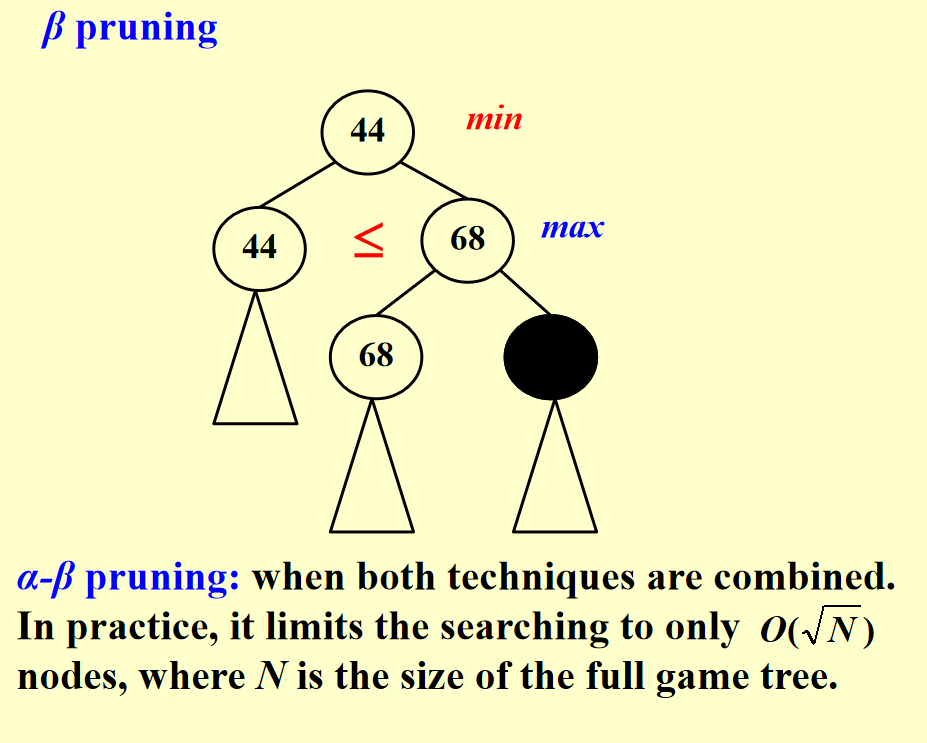
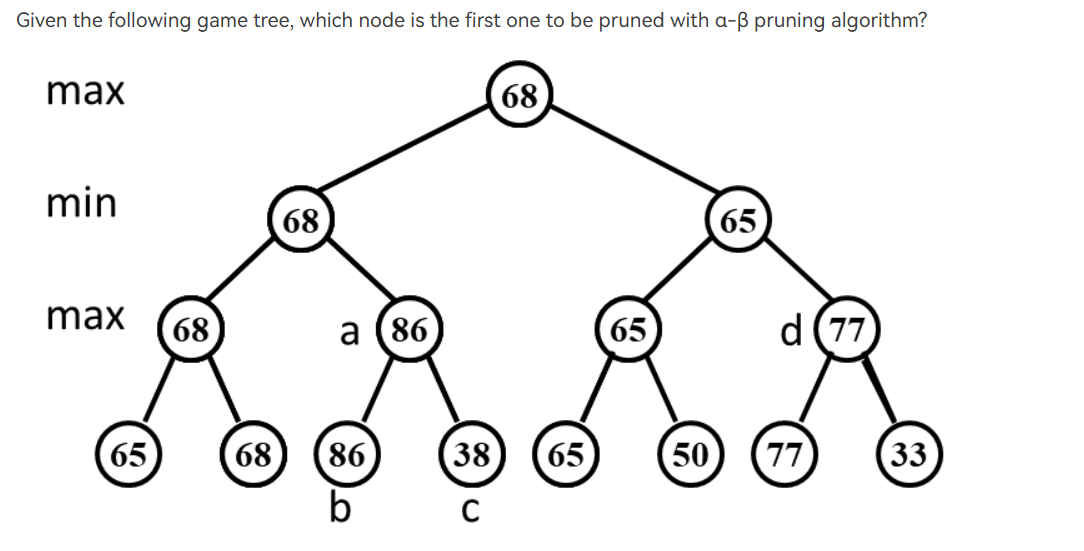
总结:当利用阿尔法贝塔剪枝时解题顺序:左子树–根–右子树(基于深度优先搜索);另外是对题目的解释,每一行后面的max和min说的其实是这一行的结果是由它的孩子max或者min得到的。
解释:在这道题目中,因为剪枝的情况是不会选用它的父亲则它被剪枝,当我们遍历知道它的父亲不选择时,此时它父亲的左孩子已经完成遍历,则右孩子被剪枝。
- 样例3 Eight Queens problem
- 8皇后问题,我们只需要在每一行中选择一个皇后,然后判断是否和之前的皇后有冲突,如果有冲突则换一个皇后,直到找到一个不冲突的皇后,然后继续在当前行的下一列中寻找下一个皇后,直到找到一个不冲突的皇后…..
- 也可以画game tree来理解解决这个问题的回溯过程。
- 样例4 the turnpike reconstruction problem
给定N(N-1)/2 distances,然后重构n个点的坐标
解决:step1:find the N;step2:x1=0(假定),x6=10;step3:find the next largest distance and check
我发现这个代码我掌握情况并不是很好,再来看看。
它的逻辑是这样的,假设我们的x0=0,那么肯定能得到最大值是确定的,我们继续接下来的操作。此时的D数组中存储的还没有重构的距离,我们找到里面的最大值,此时最大值的产生可能有两种情况:最大值由当前将要产生的坐标x(max-1)-x0;最大值由xmax-当前将要产生的坐标(x1)。我们分别前后对这两种option的子option进行检查。coding
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
bool Reconstruct ( DistType X[ ], DistSet D, int N, int left, int right )
{
/* X[1]...X[left-1] and X[right+1]...X[N] are solved */
bool Found = false;
if ( Is_Empty( D ) )
return true; /* solved */
D_max = Find_Max( D );
/* option 1:X[right] = D_max */
/* check if |D_max-X[i]|D is true for all X[i]’s that have been solved */
OK = Check( D_max, N, left, right ); /* pruning */
if ( OK ) { /* add X[right] and update D */
X[right] = D_max;
for ( i=1; i<left; i++ ) Delete( |X[right]-X[i]|, D);
for ( i=right+1; i<=N; i++ ) Delete( |X[right]-X[i]|, D);
Found = Reconstruct ( X, D, N, left, right-1 );
if ( !Found ) { /* if does not work, undo */
for ( i=1; i<left; i++ ) Insert( |X[right]-X[i]|, D);
for ( i=right+1; i<=N; i++ ) Insert( |X[right]-X[i]|, D);
}
}
if ( !Found ) { /* if option 1 does not work */
/* option 2: X[left] = X[N]-D_max */
OK = Check( X[N]-D_max, N, left, right );
if ( OK ) {
X[left] = X[N] – D_max;
for ( i=1; i<left; i++ ) Delete( |X[left]-X[i]|, D);
for ( i=right+1; i<=N; i++ ) Delete( |X[left]-X[i]|, D);
Found = Reconstruct (X, D, N, left+1, right );
if ( !Found ) {
for ( i=1; i<left; i++ ) Insert( |X[left]-X[i]|, D);
for ( i=right+1; i<=N; i++ ) Insert( |X[left]-X[i]|, D);
}
}
/* finish checking option 2 */
} /* finish checking all the options */
return Found;
}
- ex1 dfs与bfs加剪枝的速度
![hw5ex1]()
解释:
- good path其实是寻找由所有good节点构成的一条路(每个节点可能为good或者bad)
- 其实这道题可以从老师的hint中看,假设一个例子左边的叶子的深度十分深而右侧的叶子深度较浅,则我们一定存在这样的例子,当使用bfs时并没有像dfs一样遍历完那么深的深度就已经提前进行剪枝操作,则我们的时间就比dfs要短。
hw6 贪心
知识1
贪心算法的基本概念
只有当局部优解等于全局优解时可以使用;贪心算法的使用是一个逐步逼近最佳方法的过程样例1(activity selection problem)
- 这是一个常见的贪心问题,在一定的时间内有一系列活动安排,但是两个活动的进行时间不能有交叉,需要求的这个时间内所能举行的最多的活动数量。
- 寻找贪心法则:每次寻找结束时间最早的活动
- 我们想要证明我们理论的正确性,我们利用反证法,若A是按照理论取得的解,若存在一个S,但是S比A更优,我们假设A和S前t个活动都相同,那么在t+1个活动时,因为A按照最优则$f_{i(t+1)}<=f_{j(t+1)}$,则我们再后面遇到不一样时都可以用i替换j,但是最终我们会发现S不可能比A会多出活动,则假设矛盾,则我们得证。
- 时间复杂度$O(nlogn)$
- 样例2(haffuman coding)
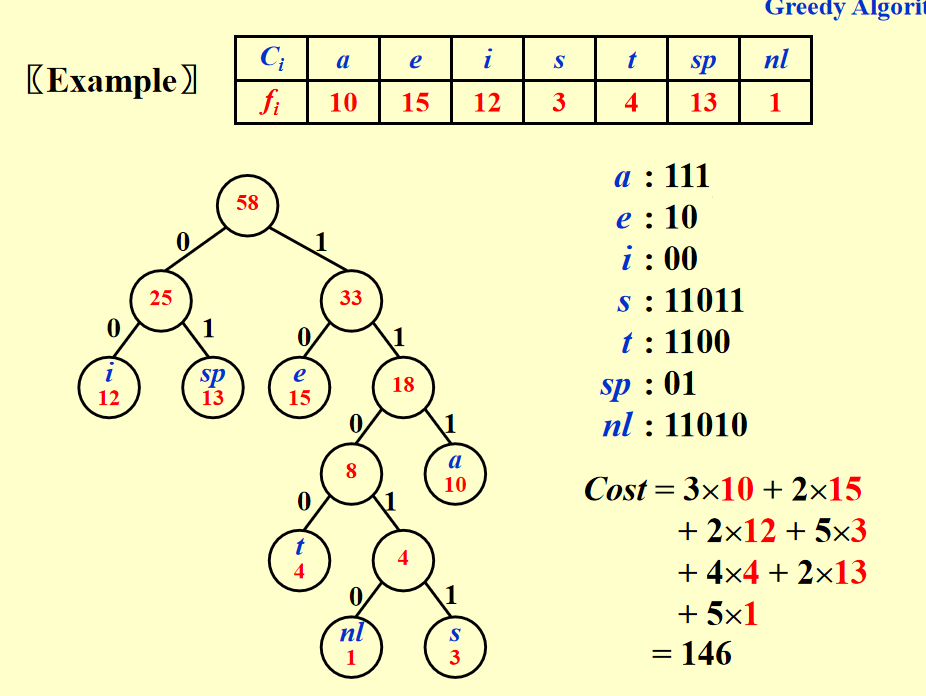
- 这一道题目我们需要寻找到一个最优的编码映射满足:the cost of $\sum_{}{}d_{a}*f_{a}$ is mininum(分别为霍夫曼树对应字符的深度和字符在字符串中出现的频次);且没有一个字符的编码是另一个字符编码的前缀(也就是说,每一个字符都在叶子上面)
- 霍夫曼解决此问题的算法如下:首先创造一系列单节点的树,然后找到两颗频次最小的树进行合并,这两颗小树则被森林删除,取而代之的是他们合并的结果,这颗大树的频次则是两颗小树频次之和。重复上述操作直到森林只有一颗树。
下面有一个ppt的样例,我觉得是频次小的放在合并的左子树![hw6zs1]()
- 时间复杂度为O(NlogN)
- 证明算法的正确性:首先有一个lamma,如果a和b是频次最低的两个字符,那么a和b在霍夫曼树中一定是兄弟。利用归纳假设加上反证法:即假定存在一棵树A,不满足霍夫曼算法但是是最优的,我们将最下层的两个结点合并得到A1,同理对霍夫曼树我们也能得到H和H1,但是在k-1个节点时我们已经知道H1是最优的,所以A不可能是最优的。
- ex1(greedy)
![hw6ex1]()
解释:其实C也很容易举出反例,因为可能存在d很大但是p很小,并且这种情况很多时当我们去到ddl很靠近的事件时已经早已逾期ddl了。我们再来正面思考情况,很容易知道
hw7 分治
知识1 counting inversion
- 定义一个数组,如果$A[i]>A[j],i<j,(i,j) is a inversion$
- output #inversion(inversion的数量)
- 若采用枚举$O(n^2)$,分治$O(nlogn)$
- 将这个数组左右等分为两半,那么所有的inversion分为三种情况(leftinversion,rightinversion,splitinversion),前两种情况的结果都可以使用递归得到,第三种情况如果使用暴力枚举其实时间还是n的平方的数量级=》优化:假如此时左右两侧都是排好序的,我们直接利用归并的merge将两侧合并,每次数量都加上左侧剩余的数量即可,那么就能在O(n)时间内解决问题。
- 总结(sort-and-countinv)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22if n<=1:
return (A,0);
else
L=lefthalf of A;
R=righthalf of A;
(B,leftINv)=sort-and-countinv(L);
(C,rightInv)=sort-and-countinv(R);
(D,spiltInv)=merge-and-countInv(B,C);
return (D,leftInv+rightINv+spiltInv);
Merge-and-countInv(B,C):
i=1,j=1,splitinv=0;
int D[n];
for k=1 to n:
if B[i]<C[j]
D[k]=B[i];
i=i+1;
else
D[k]=C[j];
j=j+1;
splitInv+=n/2-i+1;
return (D,splitInv);- 时间T(n)=2T(n/2)+O(n);->T(n)=O(nlogn)
知识2 closest pair(这个例子还没有特别熟悉)
- 首先根据横坐标分为两部分(leftpair,rightpair,splitpair)
- 当分治时,左右两侧的最小值我们都可以通过递归得到,所以现在就能产生一个较小的距离(左右两侧得到的最小值)记作$\delta$,接着我们按照上述的中轴线在水平位置$\delta$的距离形成一条带子,再对里面的每一个点以$\delta$\2为半径形成8个正方形,则每个正方形都至多有一个点(因为如果有两个点就与我们前面递归得到的结果相矛盾)
- 而当我们研究f(n),的时候,因为我们的对于当前考虑的i,其实只用考虑与它相邻的七个点,则肯定能在O(n)的时间复杂度下完成。
- 伪代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26Px:sort P by x-cord
Py:sort P by y-cord
closest pair(Px,Py)
if n<=3
final
Lx=pts on the lefthalf plane,sorted by x-cord
Ly=pts on the lefthalf plane,sorted by y-cord 在Rx和Ry的前提下都能以o(n)
Rx=pts on the righthalf plane,sorted by x-cord
Ry=pts on the righthalf plane,sorted by y-cord
(l1,l2)=closest pair(Lx,Ly)
(r1,r2)=closest pair(Rx,Ry)
$\delta$=min(d(l1,l2),d(r1,r2))
(s1,s2)=closest split pair(Px,Py,$\delta$)
return min($\delta$,d(s1,s2))
closeSplitPair(Px,Py,$\delta$):
x1=largest x-cord of the lefthalf plane;
Sx={points q1,q2.....with x1-delta<=qi.x<=x1+delta} sorted by y-cord
mindist=$\infty$;
colset=null;
for i=1 to k
for j=1 to 8
if(d(qi,q(i+j))<delta)
delta=d(qi,q(i+j))
closet=(qi,q(i+j))
知识3 分析divide and conquer的时间复杂度
$T(1)=1$;
$T(n)=a*T(n/b)$+$n^c$
recursion tree method:$T(n)=2*T(n/2)+n,T(1)=1$
上面是已知条件,下面我们画出递归树,我们发现在递归的深度为 $( k )$ 时,在前面每一层所有节点花的时间之和为 $( n )$,而最终降到最底层时的深度为 $( \log n )$,所以时间复杂度为 $( O(n \log n) )$。而我们不同的题目可能每一个节点所花费的时间有所不同,每一层的总时间可能相同 $(( n ))$,可能递减,可能递增 $(( \sqrt{n} ))$。更一般的情况:我们记根节点为第 0 层,每一个节点数量为 $( \frac{n}{b^i} )$,节点数目为 $( a^i )$,每个节点花费时间 $( a^i \left(\frac{n}{b^i}\right)^c )$。master method: 首先定义$T(N)=aT(\frac{n}{b})+f(n)$
形式一
![hw7zs1]()
主方法(master method)之所以叫“主”,是因为它分析的是 combine 和 conquer 部分孰为主导」,观察三种情况的区分条件都是比较 f(N)(每一次的 combine 开销) 和 $N^{log_{b}a}$(即求和式中的 conquer 的开销),当 f(N) 足够小时,以 conquer 开销为主(i.e. case 1);当足够大时,以 combine 为主(i.e. case 3);而其中还有一个中间状态(i.e. case 2)。
形式二
![hw7zs3]()
另外更复杂的形式,其实是f(n)的特殊形式的情况(最好能够记忆下来)
![hw7zs2]()
第三种方法(详情见毛老师的手写笔记)代换法:
首先大眼猜测最终的复杂度,然后利用归纳假设进行证明即可.先假设n/2的情况,得到一个不等式,再把不等式归纳到n的情况。需要注意的是当我们假设中含有参数c时,最终成功假设的标志是我们的不等式系数也只有与c有关而不含常数。
hw8 动态规划
样例1 weighted independent set on paths
- 考虑在一条路上,输入一系列带有权值的点,输出一系列独立(两个点之间没有公共的边)的权值之和最大的解
- 对于在n点的考虑,$S_{n}=Math.max{S_{n-1},S_{n-2}+v_{n}}$
- let c[i] be the total weight of the optical solutions of the vertcal i
- 伪代码:c[0]=0,c[1]=v[1],c[i]=max(c[i-1],c[i-2]+v[i])
- 实现方式:递归 $T(n)=T(n-1)+T(n-2)+O(1)$会存在重复计算,所以时间最终所用时长较长,或者用一个全局数组来记录c[i],每次递归我们只针对未被计算的c[i]进行计算,这样时间复杂度就为$O(n)$。若使用循环,则直接从前向后计算即可。
- 怎么计算我们是否选择v[n]呢?只需判断c[n]与c[n-1]是否相同,若相同则未选(复制c[n-1]),若不同则(c[n]=c[n-2]unionv[n]) 实现时利用递归实现即可
知识2 ordering matrix multiplication
输入:一系列矩阵,输出:对这一系列矩阵进行乘法,使得最少的运算次数
bi=#possible ways to multiply i matrixes,当我们考虑的时候通常考虑最后一次乘法时的两个矩阵的组成结构,例如四个矩阵相乘时分为:$b_{2}*b_{2};b_{1}*b_{3};b_{3}*b_{1}$。那我们此时对bn进行拆分:$\sum_{1}^{n-1}b_{i}b{n-i}$
拆分子问题:$c[i][j]$ be the minimun cost of $m_{i}*m_{i+1}….m_{j}$
$c[i][j]=min[{c[i][k]+c[k+1][j]+r_{i-1}*r_{k}*r_{j}}]$运算顺序:
1
2
3
4
5
6
7for i=1 to n
c[i][i]=0
for t=1 to n
for i=1 to n-t
j=i+t
c[i][j]=min(c[i][k]+c[k+1][j]+r[i-1]*r[k]*r[j])
return c[1][n]
知识3 dp的小题主要要观察状态转移时是否前面有未知量
知识4 背包问题
- n items 每一个都有weight和对应的价值,然后有一个容量的背包。
知识5 optimal bst
- 输入n keys并且具有相对应的频率,output:a bst with mininum average search time
hw10 np-completeness
知识1
在ppt的开头回顾了一下几个暂时不知道多项式算法的问题。- Hamilton cycle problem-NPc
- single-source unweighted longest-path problem
样例1 haltting problem
- 描述:given a programme P,an input x.Does P halt on input x?
- assume 存在 a programme Halt,Halt(P,x) return true if P halts on input x,false otherwise.
构造:Diagonal(P):if Halt(P,P)==true looping else terminate. - 我们再把构造出的diagonal展开:looping if p halts on p;halt if p loops on p;
- 但是当我们用diagonal替换P时就会发现我们前面的第二个式子的前后矛盾。则我们的假设不成立。那么这个problem不可计算。
- 对于这种不可判定问题(undecidable problem),它的特点是我们无法设计一个算法来求解它的结果。
知识2 图灵机与几个问题类概念的定义
- Turing machine: 1. $\delta(p,a)=(q,b)$ where p(now),q(next) are states and a,b(move left/right,write) are symbols.如果是确定性的图灵机则读到现在的字符,下一个状态是固定的。如果是非确定性的图灵机,它的下一个状态可以自由选取,并且如果其中某个步骤导致solution,它总是会选择这个正确的步骤(有一个最优的思想)。
- P class:指可以使用确定型图灵机在多项式时间内解决的问题(也就是我们通常意义下的可以在多项式时间内解决的问题)。
- NP class:指可以使用非确定性图灵机在多项式时间内解决的问题。这个说法等价于可以使用确定型图灵机在多项式时间内验证(判断答案是否正确)
- NPC:最困难的NP问题,所有的NP问题都可以在多项式的时间内约化到NPC(记住这个我觉得两个问题归约的困难程度便容易理解)。这样我们也看到哦,如果试图证明一个问题是NPC问题,我们可以通过证明另一个NPC问题可以多项式规约到这个问题上面。
- NPH:它不一定需要是NP问题,但所有NP问题可以多项式时间规约为NPH问题。so,$NPC=NP \subset NPH$
- 有一个小结论:Not all decidable problems are in NP.(我们其实讨论的np是decidable problems)
知识3 多项式规约
- 我们已知p含于np,但是p与np是否相等呢?
- 假如现在有两个problem x,y 若任意的实例$I_{x}$我都可以在多项式时间内映射到实例$I_{y}$,并且我的映射能保证映射前后的yes-instance性质不变
- 如果存在一个多项式时间的算法B for y,则我可以设计一个算法A for x,使得$A(I_{x})=B(F(I_{x}))$ $T<=poly(poly(I_{x}))$(因为数据规模不会超过多项式级所以我们能得到这个不等式)那么我们认为y problem更困难,并把映射叫作规约(reduction)函数,一般记作$x \le _{p}y $
样例2 汉密尔顿回路与旅行商(traveling salesman problem)
- Given a complete graph G=(V,E) with edge weights and k,is there a cycle that visits each vertex exactly once and total cost is less than k?
- 首先我们证明TSP是一个NP问题即证明TSP的解可以在多项式时间内被验证。而验证一个解是TSP问题的解,需要证明以下两个点:这条路径经过了所有节点恰好一次,且总成本小于k。显然在多项式时间内能验证。
- 我们现在尝试按照知识3,寻找一个规约联系汉密尔顿圈与TSP问题:首先TSP问题基于完全图,我把汉密尔顿原图存在的边设为1,补的红边设为2.$k=|V|$。解释:如果G有一个汉密尔顿圈,在$G^{.}$中的cost肯定不超过k,否则$G^{.}$的cost肯定超过k,所以不存在。所以左右两侧的yes-instance属性满足,我们的规约没有问题。
样例3 Circuit-SAT
- 它是最早被证明是NPC的问题
- 解释:这个问题就是判断一个具有n个布尔变量的布尔表达式是否具有结果为True的解。
- 3-SAT是这个问题的特例,它对布尔表达式的形式有特殊要求。(三个一组的形式)
知识4 A formal-language Framework
- 对于一个问题,所有instance组成集合I,对应的solutions组成集合S。则problem(i)=s.对于决定性问题(我们以path代称):For every i in I,path(i)=1 or 0;
- 编码:我们通过一个映射map把instance编码成二进制字符串的表达形式
- 因为我们的p和np的定义其实就是基于决策问题,所以我们接下来都是基于decision problem来分析
3.1 an alphabet $\sum$ is a finite set of symbols
3.2 A language L is any set of strings made up of symbols :L={$x \in \sum : Q(x)=1$}
3.3 我们定义empty string:$\epsilon$ 定义empty language $\phi$ - 我们再用language的思想来定义P:P = { L ⊆ {0, 1}* : there exists an algorithm A that decides L in polynomial time }
- 我们用language的思想定义NP:A language L belongs to NP iff there exist a two-input polynomial-time algorithm A and a constant c such that L = { x ∈ {0, 1}* : there exists a certificate y with |y| = O(|x|^c) such that A(x, y) = 1 }. We say that algorithm A verifies language L in polynomial time.
知识5 多项式时间的算法
An algorithm A has a polynomial-time running time if there exists a polynomial p(n) such that the running time of A on an input of length n is bounded by p(n).知识6 多项式时间可验证
- we say V is an efficient verfier from problem x if
- V is a polynomial-time algorithm that takes two arguments:an instance I of x and t
- for any instance I of x ,I is a yes-instance if and only if there exists a proof t with $|t|<=poly(|I|)$ and V(I,t)=1
- 则problem多项式时间可验证
知识7 汉密尔顿圈问题(例子)
- Given a graph G=(V,E),is there a Hamiltonian cycle(恰好经过每个顶点一次) in G.
- $t=v_{i1},v_{i2},…,v_{in}$
- V(I,t):test每个顶点是否都在t中出现一次,if no return;再看每个顶点相邻两边是否有边,都满足 return 1
- 我们再对照前面的多项式时间可验证的定义,则hamiltonian cycle NP-complete
样例4 clique problem(npc) and vertex cover problem(npc)(例子)
- clique problem:Given a graph G=(V,E) and k,is there a subset of V with size >=k such that every two vertices in the subset are connected by an edge?(这个subset为完全图)
- vertex cover problem:Given a graph G=(V,E) and k,is there a subset of V with size <=k such that each edge in E is incident to at least one vertex in the subset?(每一条边都至少有一个顶点在subset中)
- 我们先要证明顶点覆盖问题为NP问题,则只需要验证一个解是否满足顶点覆盖,我们在$O(N^3)$能完成
- 我们现在尝试规约团问题与顶点覆盖问题。如果在左边的实例$V^{.}$是一个团,那么右边$V-V^{.}$是一个顶点覆盖。
hw11 approxiamtion
- 补充知识 卷积
- 现在有两个长度为n的向量A和B,它们的卷积是长度为2n的向量,且$c_{k}=\sum_{i+j=k}^{} a_{i}b_{j}$
- A=a0+a1x+a2$x^{2}$…..
B=b0+b1x+b2$x^{2}$…..
若将A和B相乘,$AB=c0+c1x+….$其实不难发现这里得到的ci与我们前面定义的卷积一一对应。但是现在我们的时间复杂度还是较高,但是我们运用快速傅里叶变换能够把时间复杂度压缩到$O(nlogn)$ - 首先我们表示一个多项式除了使用常见的系数多项式,也可以用点值多项式,即在函数图像中一个多项式被n个点唯一确定。
- 知识1 近似算法
given an algorithm A for any instance I,$max{\frac{A(I)}{opt(I)},\frac{opt(I)}{A(I)}} \leq \rho$,then A is a $\rho$ approximation algorithm,$\rho$ is approximation ratio.($\rho$越接近于1,则说明结果越接近准确值)
知识2 近似范式
approximation scheme指的是对于某个优化问题的一族相同模式的算法,它们满足对于确定的$\epsilon$ 算法的近似比为$1+\epsilon$。此时这一族的算法的复杂度可以表示为$O(f(n,$\epsilon$))$,当其关于n是多项式时,我们称其为多项式时间近似范式(PTAS),当其关于n和$\frac{1}{\epsilon}$都是多项式时,我们成为完全多项式近似范式(FPTAS)样例1 背包问题
- 背包问题的分数版本我们利用贪心肯定能找到optimal solution,下面我们重点考虑(0-1 version),这也是np complete问题。
- 贪心做法:则我们总是选择可以放得下,还没放进去的$\frac{p_{i}}{w_{i}}$最大的进去,此时的近似比为2
- 贪心做法证明过程:我们用pmax表示所有 item 中最大的利润,Poptimal
表示准确解,Pgreedy表示我们使用贪心做法得到的答案。在该问题中,近似比的计算表达式为:$\rho=max(\frac{P_{optimal}}{P_{greedy}},\frac{P_{greedy}}{P_{optimal}})$
$p_{max}\leq P_{greedy}$
$P_{optimal}\leq P_{greedy}+p_{max}$根据以上两个不等式可以证明相似比的正确性 - 动态规划做法:定义$C[i][j]$=最小的背包量来实现价值j(并且只考虑前i个物品),此时的时间复杂度$O(n\sum v_{i})=O(n^2v_{max})$但是还是一个伪多项式算法.
我们再设置一个d,$d=\frac{vmax}{n} * \delta$,我们再把所有的value都除以d,并取上整(scading).这一步骤结束后,我们能保证所有的value都是整数,此时我们将d代入就会发现现在的$vmax=O(\frac{n}{\delta})$,并且我们可以通过证明得到不等式
$v(S) \leq d \cdot v’(s) \
\leq v(s) + v_{\text{max}} \cdot \delta$
我们接下来研究最优解,在scading后的最优解在scading的value的情况下肯定是优于原问题的最优解在scading的value的,$v(scadding) \geq v(before scadding)-vmax*\delta \geq (1-\delta)v(before scadding)$
则是FPTAS
样例2 k-center problem
- 描述:K 中心问题指:给定平面上的一系列site,在平面中找出k个不同的center,记$site_{i}$到离它最近的center的距离为$dis_{i}$,求$max{dis_{i}}$的min
- 问题转化:平面上有一堆点,我们要在上面找k个中心去画圆,使得这k个圆能覆盖所有的点,现在要求最大的那个圆的半径最小能多小。
- Naive Greedy:我们每次都选择最可能成为中心的那个点(如果是第一个点,就选取所有点的中心;如果不是第一个点,就选取能一个最能让r(C)下降的)
- 2r-Greedy:在这个问题中我们可以迁移这个思想,即先猜一个r,然后尝试用k个半径为r的圆去覆盖剩下的所有点。
- 2r-Greedy的宽泛必要条件筛选:设$C_{x}$表示选中的center,$S_{x}$表示尚未被任何圆覆盖的site,$r_{x}$表示当前二分出来的,要我们判断的半径,S依然表示所有site的集合:
1.初始化$C_{x}=0$;
2.当还有点没被覆盖时,重复这些操作:
a.随机选取一个site,$s_{i}\in S_{x}$,将其插入$C_{x}$,并在$S_{x}$删除$s_{i}$
b.删除Sx中所有距离si不足rx的点
3.当所有点都被覆盖后,如果$|C_{x}|\leq k$,返回yes,否则返回no。当我们进行这个条件筛选后,如果返回yes,则下一个$r_{x}$应当选取更小,返回no,下一个半径应该取大。 - 现在我们再分析一下我们上面的宽泛必要条件筛选算法,这是一个启发式的做法,旨在每次寻找还没被覆盖的点作为新的center,用一个半径为2rx的圆去覆盖剩下的点,要更好地解释这个启发式做法的内核我们需要证明一个lamma。
- lemma:假设半径为r,以c为圆心的圆C覆盖了S中的所有点,那么对于固定的半径$r^{.}$,要想取任意的$s_{i} \in S$为圆心,形成的圆$C_{i}$,总是能覆盖S中的所有点,则$r^{.} \geq 2r $,这个引理的证明不要求掌握,但是它的附加结论就是:以r为半径的最优覆盖圆,一定能被任意$s_{i}$为圆心,2r为半径的圆覆盖
- 当我们明白了上面的lemma以后,我们就可以根据我们的算法得到一个最终的$r_{x0}$,满足$r_{x0}\leq r(C^{*}) \leq 2r_{x0}$,此时显然易见近似比为2
- Smater Greedy:我们可以优化一下上面的启发式算法的策略,但是并没有改变内核,所以近似比还是2.
算法进程如下:
1.初始化$C_{x}=0,S_{x}=S$
2.随机选取一个site $s_{i}\in S_{x}$,将其插入$C_{x}$,并从原来的$S_{x}$删除
3.当$|C_{x}| \leq k$且$S_{x}$不等于空重复操作:
a.选取一个site $s_{i} \in S_{x}$,它满足$\forall s_{j} \in S_{x},dis(s_{i},C_{x}) \geq dis(s_{j},C_{x})$(即这个点是还没被覆盖的点中距离$C_{x}$最远的点)
b.将$s_{i}$插入$C_{x}$,并在未覆盖的点的集合中将其删除
4.如果$|C_{x}|\leq k,S_{x}=\emptyset$,return yes - In metric space(度量空间):
常见的欧几里得空间也属于度量空间的一种,而度量空间满足如下性质:
1.$dis(x,x)=0$
2.$dis(x,y)=dis(y,x)$
3.$dis(x,y) \ leq dis(x,z)+dis(z,y)$ - 对于k中心问题只能达到2近似,不能进一步提高准确性,除非P=NP(如果我们能够得到2-$\epsilon$ approximation,then we can solve DOMINATING-SAT in 多项式时间)
样例3 approximate bin packing(该问题的决策形式–NP hard complete)
- 解释:装箱问题是指给定N个item,每一个item都对应一个size($0 \le size \leq 1$),一个bin的大小为1,尝试寻找最少的,能够装载所有item的bin的数量。对于这个问题的解决,我们提供三种近似算法,需要注意的是当我们处理$item_{i}$时我们不知道后面的item的情况(online)
- online:Next Fit
1.NF策略总是选择当前最后一个bin,若如果容纳,则将当前item放入其中,否则新开一个bin。NF策略总是使用不超过2M(准确解)-1个bin
2.证明:假设用了$B_{1},B_{2}…B_{2k}$个箱子,其中$s(B_{i})$表示第i个箱子中装的物体的size之和,则
$s(B_{1})+s(B_{2})\ge 1$….
$\sum_{i=1}^{2k}s(B_{i})\ge k$则能得到OPT(最优解所使用的箱子数量)>k
3.我们可以找一个实例,有4n个物品,$\frac{1}{2},\delta,\frac{1}{2},\delta…$,通过NF我们需要2n个箱子,但是最优解是n+1
4.此时我们称NT是tight,不可能表现更好了 - online:First Fit
FF(can be implemented in $O(NlogN)$)策略,按照item的顺序,总是选择第一个能放下item的bin,若所有bin都无法放入,则新开一个bin。FF策略总是使用不超过[1.7M]个bin - online:Best Fit
BF策略,按照item的顺序,总是选择能够容纳当前item且剩余空间最小的bin,若所有bin都无法容纳当前item,则新开一个bin。BF策略总是使用不超过[1.7M]个bin - 小结论:对于装箱问题,如果限定使用在线做法,则最优的近似解法的最坏情况也至少需要准确解的$\frac{5}{3}$
- offline:First Fit Decreasing
离线做法的优势在于它能够获得所有item的信息以求统筹归化,这里给出的近似做法是将item按照size降序排序,再使用FF or BF。FFD(BFD)策略总是使用不超过$\frac{11}{9}M+\frac{6}{9}$,此时的绝对近似比为$\frac{3}{2}$ - 小结论,没有多项式算法能够做到绝对近似比比$\frac{3}{2}$好,除非P=NP
ex1
![hw10ex1]()
解释:正确答案:F。这道题目是一个典型的approximation的问题,但是当时确实始终没有想明白。首先我们知道Vertex Cover问题有一个2-approximation的算法,即最差情况也被限制在2倍最优解中。我们现在已知的是Clique problem能够多项式规约到Vertex Cover问题(还是不太理解这个题目)ex2
![hw10ex2]()
解释:正确答案:CD。又是毛老师的经典多选题,G是无向不含负权值的图,先分析最大伸展树,也就是最小伸展树的相反面,但是仍然不形成圈。而这道题目定义的$S_{G}={max(v):v\in V},max(v)$be the maximum-weight edge incident to v.其实当时选错时确实没有认真分析各个例子来得到答案,最简单的例子就是例如有四个点形成三条边,则$T_{G}$一定有三条边,则$S_{G}$最少可以有两条边,但是我们可以发现在这种边较少的情况下,缺少的那一条边的权值一定不是最大的,我们可以粗略的感受随着顶点数增加是,2倍关系的约束仍然存在。
hw12 Local Search
知识1 核心思想
找到一个可行解,以及量化其优程度的目标函数,再在这个可行解上寻求优化,直到达到局部最优解。其实就是拆分成local(邻居更好我们就到邻居去)和search(邻居都不够好时就停止)样例1 vertex cover problem
- 解释:给定一个无向图,找到一个最小的顶点集合,使得每条边都至少有一个端点在S中。
- 将这个problem进行抽象:解空间是所有顶点覆盖的集合,每个解的函数值是这个解的顶点数量。
- 我们采用local search来解决问题,首先的可行解是所有的顶点的集合,我们对于一个解S,定义它的邻居$S^{.}$可以通过S加一个顶点或者删除一个顶点得到。
- local search:
1.S=V
2.if S-{u} is a vertex cover
3.S:=S-{u}
4.return S - 但是这种local search得到的结果可能很差
知识2 优化(Metropolis algorithm)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18SolutionType Metropolis() {
Define constants k and T;
Start from a feasible solution S \in FS ;
MinCost = cost(S);
while (1) {
S’ = Randomly chosen from N(S);
CurrentCost = cost(S’);
if ( CurrentCost < MinCost ) {
MinCost = CurrentCost; S = S’;
}
else {
With a probability e^{-\Delta cost / (kT)}, let S = S’;
else break;
}
}
return S;
}知识3 模拟退火算法(simulated annealing)
样例2 Hopfield Neural Networks
- 解释:输入一个带权的图,现在要对顶点进行赋值(1或-1),如果我们说一条边是好的:若weight为正,端点的正负号相反;若weight为负,端点的正负号相同。也就是说,这条边的weight乘以两个端点的值为负时,边是好的。我们的目标是找到这样对顶点的赋值,使得整张图好的边的权重的绝对值之和最大。(social welfare)
- 而对于某个节点u,它希望和它相邻的好边的权重之和最大。(utlity of u)
- 我们现在想要找到一个赋值,对于每个点都是满意的我们说这是均衡的。
- state-flipping algorithm
4.1 随便挑一个赋值
4.2 while some nodes are not satisfied(改变后收益增加)
4.3 flip the state of u
4.4 return s - 下面给出证明:$\Phi(s)=\sum_{e is good in S}|w_{e}|$
当我们进行flip的时候,我们假设翻转$u$,$\Phi(s^{.})=\Phi(s)-\sum_{e is good in S incident to u}|w_{e}|+\sum_{e is bad in S incident to u}|w_{e}|$ 我们可以看见Phi增加,而上限就是所有边的权重之和。则证明可以看出这是一个local search算法,并且在有限轮结束循环。 - 再次理解这个问题,若现在图里面的边全是正的,则我们就相当于将图中所有的顶点划分为A,B两个子集,而此时好边就是一点在A,一点在B。$\delta(A,B)={(u,v)\in E|u \in A,v \in B}$,现在我需要找到上述边的权重之和最大,此时转化为Maximum cut problem.
样例3 Maximum cut problem
state-flip-mmax-cut
1
2
3
4
5
61.1 随便找一个(A,B)
1.2 while some node u is unsatified
($\sum_{e is a cut edge incident to u}w_{e} \le \sum_{e is not a cut edge incident to u}w_{e}$)
flip the state of u
return (A,B)
1.3 in O(w) iterations return a stable(A,B)
我们来证明一下,for $u \in A$,$\sum_{e=(u,v) \in E,v \in A}w_{e} \leq \sum_{e=(u,v) \in E,v \in B}w_{e}$,我们再对每个u进行求和,那么可以得到,$2\sum_{e=(u,v) \in E,u\in A,v\in A} \leq w(A,B)$,
$\sum_{e \in E} w_{e}=$三种顶点情况的边之和,
$\leq \frac{1}{2}w(A,B)+\frac{1}{2}w(A,B)+w(A,B)$
则我们可以得到上面算法local search的值(w(A,B))至少是最优解的一半Idea:发生翻转时仅仅在有大的改进时才发生,大的改进($w(A,B)$ inceases by a factor of $\geq 1+\textbf{2}\frac{\epsilon}{|V|}$)(要注意前面的系数),其中epsilon为一个参数,则我们的循环现在需要$O(\frac{n}{\epsilon} logw)$,此时可以证明解的质量为最优解的$\frac{1}{2+\epsilon}$(有机会可以补充一下证明过程)
(终于忙完所有的实验可以静下心来思考一下):首先我们需要注意我们只有当有大的改进(并且这个大的改进是针对我们当前得到的$w(A,B)$),我们才进行翻转操作。
则在最终情况下,我现在的所有点都已经达到最优情况了不再需要翻转,也就是说,再最终情况下,对A集合内的任意一点u,均满足:
$\sum_{e=(u,v) \in E,v \in A}w_{e} \leq \sum_{e=(u,v) \in E,v \in B}w_{e}+\frac{2\epsilon}{|V|}w(A,B)$
那么我们将每个所有A中的u的上述表达式进行求和,我们可以得到:
$2\sum_{e=(u,v) \in E,u\in A,v\in A} \leq w(A,B)+\frac{2\epsilon}{|V|}|V_{A}|w(A,B)$
我们也可以将同样的操作用在集合B的身上:
$2\sum_{e=(u,v) \in E,u\in B,v\in B} \leq w(A,B)+\frac{2\epsilon}{|V|}|V_{B}|w(A,B)$
而我们默认最优的解就是等于所有边的权重之和(理论上有这种赋值存在):
opt=$\sum_{e \in E} w_{e}$
$\leq w(A,B)+\frac{1}{2}w(A,B)+\frac{\epsilon}{|V|}|V_{A}|w(A,B)$
$+\frac{1}{2}w(A,B)+\frac{\epsilon}{|V|}|V_{B}|w(A,B)$
$=2w(A,B)+\epsilon w(A,B)$我怎样提高我的local search呢?我们可以考虑增大邻域(允许翻转k个节点,而不是只翻转一个节点),但是每一步所消耗的时间也变多$O(n^{k})$
ex1
![hw11ex1]()
解释:这一道题是想使用local search解决k-center问题,我们的想法是先将所有的点进行分类,对于某个指定的中心,如果他们都离这个中心是最近的,这些点就被划分到这个类中。而我们的local search就是对这些划分好的类选择类的最中心作为新的centre。
如果以上操作并不能使最终的结果半径减小,那么我们的操作就会停止。当然选择这个答案还是比较容易,因为k-centre的近似比不能做到小于2,但是这个算法的近似比是否为2呢?其实这道题我觉得考察的重点就是让你明白这个方法的内核与我们在approximation章节里面介绍的(通过没有被覆盖的site作为新的centre,利用一个lamma证明近似度为2)算法的内核不同,从而明白这个题目的近似度并不是2.ex2
![hw11ex2]()
解释:其实这一道题目的题意我不是特别的清晰。题目里面的sizes of the search space我觉得还是有必要理解的,对应的是local search算法中的解空间。首先对SAT问题(给定一个布尔逻辑表达式,判断是否存在一种变量的赋值使得整个表达式为true)进行分析,则很容易知道解空间的大小为$O(2^{n})$,同样如果我们不考虑剪枝,N皇后问题的解空间大小也为$O(n^{n})$
hw13 Randomized algorithms
样例1 Hiring problem
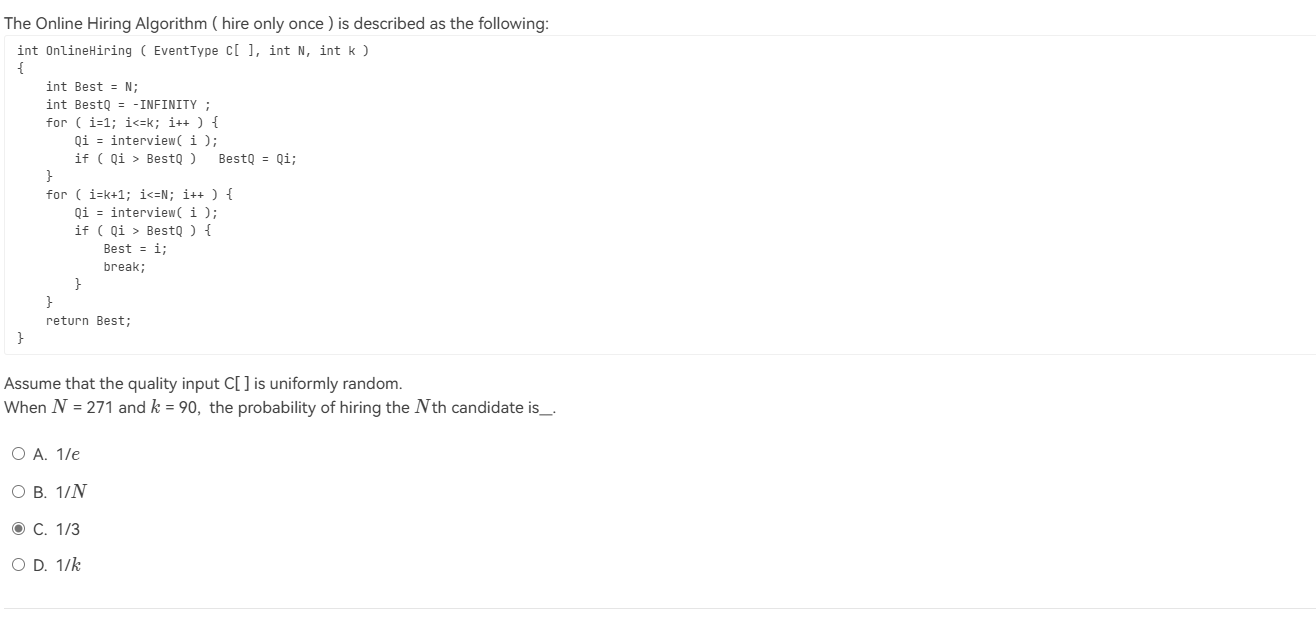
- 问题解释:有n个候选人,对于每一个候选人,面试完毕立刻做决定。目标:想要招到最好的人;雇佣尽可能少的人。
- 任意一个确定性算法,最坏情况下所有人都得雇佣。
- 我们接下来证明用随机算法雇佣$1+ln(n)$ in expectation
- 首先在面试前,对候选人随机排序,排完序之后从前往后面试即可。如果面试者是目前的最好的,我就雇佣他。
我们采用随机变量$X_{i}$表示第i个人是否被雇佣,那么$X_{i}$的期望为$P(X_{i}=1)=P(X_{i}=0)$=P(condidate i is the best among the first i candidates)=$\frac{1}{i}$,那么$E[X]=\sum_{i=1}^{i=n} \frac{1}{i} \leq 1+\int_{1}^{n}dx \frac{1}{x}=1+ln(n)$,类似的办法我们可以求出下界,为ln(n+1) - 现在再给出一个直观的算法:
5.1 随机排序
5.2 面试前k个
5.3 for i=k+1 to n
if candidate i is the best among the first k candidates
hire i
break
此时的Pr[the best candidate is hired]=$\sum_{i=k+1}^{n}$ Pr[the best candidate is a position i and candidate i is hired]=$\sum_{i=k+1}^{n} Pr[A_{i}B_{i}]$=$\frac{1}{n} \sum_{i=k+1}^{n} Pr[B_{i}|A_{i}]$ 则我们想要雇佣i,那么前i-1个人最好的一定出现在前k位
$=\frac{1}{n} \sum_{i=k+1}^{n} \frac{k}{i-1}\geq \frac{k}{n}ln(\frac{k}{n})$
则我们想要找到最大值,当k=e时有最大值。
样例2 Quick sort
- 算法概览:
if $|A|\leq 3$:
frivial
else
choose a pivot p from A
A1={a:a小于p}
A2={a:a大于等于p}
QuickSort(A1)
QuickSort(A2)
output A1,p,A2 - 时间复杂度的保证:通常满足:$\frac{3}{4}|A|\geq |A1|,|A2| \geq \frac{1}{4}|A|$,此时是好的pivot并能保证O(n)的时间复杂度
- 当我们随机取pivot,如果是good则收下,否则再取。total:$O(nlogn)$ in expectation
- Idea:随机取pivot,无论好坏都继续下去,可以证明这样的总时间还是$O(nlogn)$
- 算法概览:
样例3 MAX3SAT
- 问题解释:给定一个公式,求解公式中变量的取值使得公式为true。
- 对于每一个括号,令Y为满足条件的括号数量,则$E[Y]=\frac{7}{8}k$
$
E[Y] = \sum_{i=0}^{k} i \cdot \text{Pr}(Y = i) = \sum_{i=0}^{\left[\frac{7}{8}k\right]} i \cdot \text{Pr}(Y = i) + \sum_{i=\left[\frac{7}{8}k\right] + 1}^{k} i \cdot \text{Pr}(Y = i) \leq \frac{7}{8}k \cdot \text{Pr}\left(Y \leq \frac{7}{8}k\right) + k \cdot \text{Pr}\left(Y \geq \frac{7}{8}k\right)
$
ex1
![hw12ex1]()
解释:这一道题目是关于快速排序的随机形式,首先我们需要理解快速排序法的内核,就是通过选取一个pivot,然后把小于pivot的元素放在左边,大于等于的元素放在右边,然后对左右两个子数组递归进行快速排序。此时假定我们已经选择了$a_{i}$或者$a_{j}$作为pivot,但是我们并不知道各自的大小,无法计算概率。ex2
![hw12ex2]()
解释:这一道题其实最主要的是找到关联方程,假设我们对N个nodes的链表设需要E(N)个步骤,则能得到下列的关系式,因为我们每一次会进行一次删除操作:
$E[N]=\frac{1}{n}\sum_{i=1}^{n-1}E[i]$+1;我们发现,E[1]=1,
E[2]=1+$\frac{1}{2}$(E[1])=1+$\frac{1}{2}$;我们可以证明:$E[N]=\sum_{i=1}^{n}\frac{1}{i}$,由级数求和的知识可以得到$\Theta(logN)$ex3
![hw12ex3]()
解释:这道题我觉得我错误的原因是没有彻底搞懂,这个online hiring的逻辑(对于最后一个求职者,因为我们必须选择一个则无论他怎么样我们都得选择他。)弄懂了这一层逻辑,我们在这里只需要考虑前面的270个求职者的分布,我们只需要让他们都不被选择就好。说明他们当中最厉害的人在前k个里面,$P=\frac{90}{270}=\frac{1}{3}$
hw14 并行算法
知识1 计算模型
- random access machine
1.1 memory: an infinity sequence of cells(其中的每一个都有一个地址,可以存储一个整数)
1.2 cpu:处理器用来做运算;里面有若干个寄存器;可以做四种最基本的操作(每一种都消耗o(1)时间):init,运算,比较,读写内存。 - PRAM
2.1 memory
2.2 multiple processors:此时涉及并行,存在三种模型。
2.3 EREW(不能同时读写)
2.4 CREW(可以同时读但不能同时写)(最常见)
2.5 CRCW(可以同时读也可以同时写) - 处理冲突的三种方法
- random access machine
样例1 前n个数的和
- 问题介绍:返回n个数的和
- 想法:可以按照一颗树的形式两两求和,并往上计算。则这棵树的层与层之间无法并行,所以总共我需要$O(logN)$
知识2
- $T_{P}(N):running time with p processors on input size of N$
- $T_{1}(N)$=总工作量w(N)
- $T_{无穷}(N)$:最长的链(上面的节点无法做并行运算)的长度,也可记为$D(n)$
- $T_{p}(N) \geq D(n) T_{p}(N) \geq \frac{w(N)}{p}$
$T_{p}(N) \leq \frac{w(N)}{p} + D(N)$
我们可以得到$T_{p}(N)=\Theta(\frac{w(N)}{p}+D(N))$
我们接下来证明一下:我们首先将所有的工作拆分成D组,每一组我们都有$T_{pi} \leq \frac{D_{i}N}{p}$取上整,
则进行求和可以得到最终的不等式。
样例2 prefix sum
- 问题介绍:prefix sum:给定一个数组,求出每个位置之前的和。
- 采用并行来处理:我们可以结合我们的样例1采用并行处理,相当于我们对于这n棵树进行并行计算(而里面的每一棵树都是采取并行进行计算的)。此时我们的总工作量为$O(n^2)$深度为$O(logn)$.
- 我们再给出一个更优秀的并行算法:我们给树进行赋值$C(h,i)=\sum_{j=1}^{\alpha}A(j),A(\alpha)$是以C(h,i)为根的子树的最右侧的叶子。
此时我们能够发现$C(h,1)=B(h,1)$ for any h
我们再寻找C之间的关系,不难发现,如果C(h,i)是一个right child
$C(h,i)=C(h+1,\frac{i}{2})$
如果是一个left child $C(h,i)=C(h+1,\frac{i}{2})+B(h,i)$
那么我们就能从上往下更新我们的C,从而降低我们的总工作量。此时我们的总工作量为$O(n)$深度为$O(logn)$
样例3-归并排序
- divide conquer merge
- 分析 总工作量 深度
divide O(1) O(1)
conquer 2w(n/2) O(n/2)
merge O(n) O(n) - 我们怎么优化我们的算法(我们重点考虑对两个有序的数组的归并操作)
3.1 给定两个数组A,B
3.2 rank(i,B):rank of A[i] in B;rank(j,A):rank of B[j] in A
3.3 for i=1 to n-1
C[i+rank[i,B]]=A[i]
C[j+rank[j,A]]=B[j]
则此时w(n)=O(n),D(n)=O(1)(在我们得到rank数组的前提下) - 现在我们的问题转化为怎样得到这个rank数组。因为此时A,B已经排好了序,则我们进行二分查找操作即可。w(n)=O(nlogn),D(n)=O(logn)(w(n)过大)
- 当然另外一种得到rank数组的方式是serial Ranking。通过双指针移动遍历两个数组,此时的w(n)=D(n)=O(n+m)(D(n)过大)
- 我们给出最终的算法–Parallel Ranking
6.1 stage 1:Partitioning:得到$p=\frac{n}{logn}$(拆分的组的数量)
6.2 stage 2: Actual Ranking
A_select(i)=A(1+(i-1)logn)
B_select(i)=B(1+(i-1)logn)
Compute Rank for each selected element
详细描述一下:相当于每个小组都只有$log(n)$的元素,然后对这些元素分别对整个大小为n的另一个数组作rank,$W=O(plogn)=O(n),T=log(n)$
现在我们有2p个小组,组与组之间是并行的。并且我们现在的rank信息都知晓了,就能进行merge操作。$T=O(logn),W=O(n)$
样例4-Maximum Finding
- 问题介绍:找到最大数
- 我们串行计算:W=O(n),T=O(n)
- binary tree–两两比较从树的底部移动到上方,此时的的W=O(n),T=O(logn)
- comparing all pairs:
for Pi , 1 $\leq$ i $\leq$ n pardo
B(i) := 0
for i and j, 1 $\leq$ i, j $\leq$ n pardo
if ( (A(i) < A(j)) || ((A(i) == A(j)) && (i < j)) )
B(i) = 1
else B(j) = 1
for Pi , 1 $\leq$ i $\leq$ n pardo
if B(i) == 0
A(i) is a maximum in A
此时T=O(1),W=$O(n^2)$ - divide-and-conquer
5.1 先划分成$\sqrt{n}$组,我们再递归(所以最后并行时间与总消耗的计算应该按照类似分治画递归树的方式计算)地找到每一组的最大数(在这里我们使用comparing pairs计算),我们再找到这$\sqrt{n}$个数中的最大数。
5.2 $w(n)=\sqrt{n}w(\sqrt{n})+O(n)$ w(n)=O(nloglogn)
$T(n)=D(\sqrt{n})+O(1)$ T=O(loglogn) - 我们再优化这道题目。
6.1 我们把n个数划分成k组,然后串行地解决每一组,T=O(n/k),W=O(n)
6.2 对于我们得到的k个数我们再使用前的divide-and-conquer的算法。此时W=O(kloglogk),T=O(loglogk)
6.3 W=O(n+kloglogk),T=O(n/k+loglogk),let $k=\frac{n}{loglogn}$,W=O(n),T=O(loglogn) - Random Sampling–W=O(n),T=O(1)
7.1 这是一种随机算法,不一定能成功,但是成功概率较高为$1-\frac{1}{n^c}$
7.2 先从n个数里面随机挑出$n^{\frac{7}{8}}$,然后再在这个组中挑出最大的数m。
7.3 再在A中找到不小于m的数,寻找最大值
7.4 现在我们的重点是如何挑出m:我们将这个$n^{\frac{7}{8}}$大小的组划分成$n^{\frac{3}{4}}$个group,对每一个group用comparing all pairs来解决。现在我们就得到了$n^{\frac{3}{4}}$个数,我们再把它划分成$n^{\frac{1}{2}}$个group,对每一个group用comparing all pairs来解决。我们肯定能保证T=O(1),W=O(n)
hw15-External Sorting
样例1
- 注意run是内部已经排好序的internal memory
- 每个run的长度为M,#runs=$\frac{N}{M}$,#merge operations=1+$log_{2}\frac{N}{M}$,我们也把#merge operations称作#passes
- 当然我们的merge不一定需要2合1,我们可以采用k-way merge(能够有效降低#passes)此时的#passes=$1+log_{k}(N/M)$,但是这样我们需要2k tapes(我们每一次pass的时候都需要k个tape来存放每一路的序列,而每一路都被我们划分成了k份,则还需要k个tape来存放我们这一次pass得到的结果)
![hw15zs1]()
- 我们现在想要使我们使用的tapes减小,这里给出两种想法,但是我们为了避免copy,我们通常在最初不等分配。
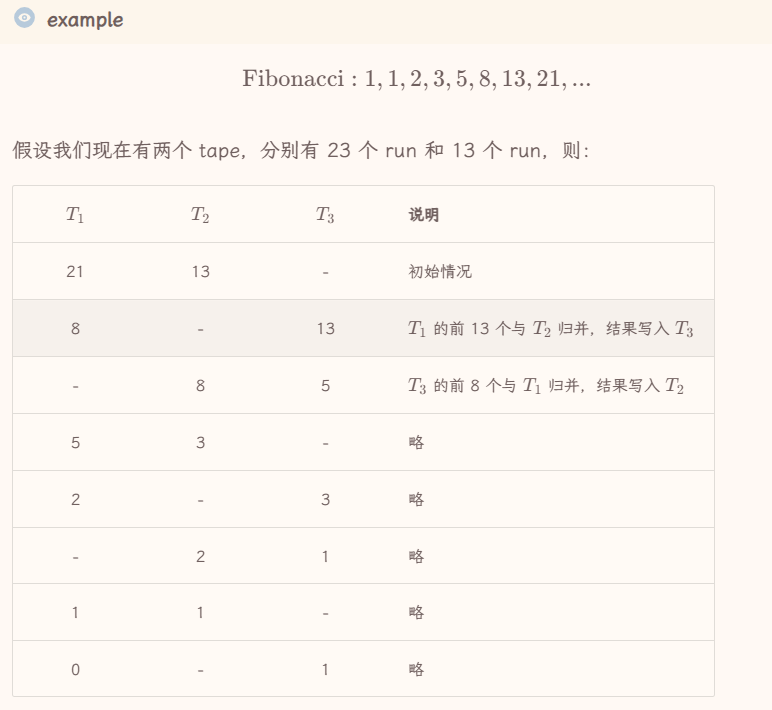
知识2–不等分配与斐波拉契序列
- 按照斐波拉契数列的项来分配每个tape的run的数量,此时每一次pass只需要一个空闲的tape。当然如果最初的run的数量并不是斐波拉契序列,我们就可以补充一个空白格补充到斐波拉契序列的情况。
- 例子
![hw15zs3]()
- 如果我们延伸到k-way的merge,我们就需要构造k阶斐波拉契数列,然后按照这个数列来分配每个tape的run数量。
知识3–获得更长的run
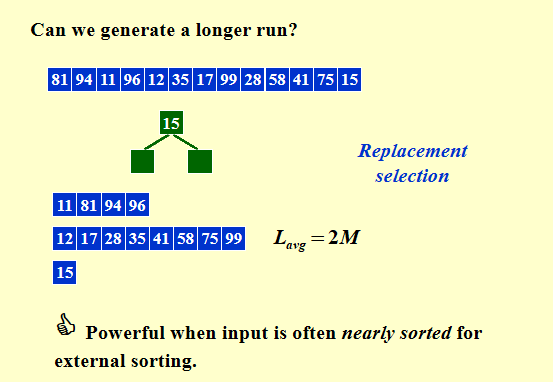
- 为什么我们要想进行这个操作,因为我们想要减少pass的数量,但是单纯地增加k的量会导致tape的需求增加,也会导致内排序的复杂度增加。我们这里就想要生成比M大的初始run,相对减少pass的数目。
- 我们采用replacement section的策略
- 比如给定一个数组,我们找每三个数中的最小值,如果这个最小值比当前的run的最大值要小,那么这个最小值我们还是保存在这三个数中并标记一下,当此时的这三个数都被标记时就说明这三个数其实属于下个run。
![hw15zs2]()
知识4–外部排序中的buffer(并行优化)
- 这里并行的目标是让读操作不阻塞用操作,用操作不阻塞写操作。在之前的外部排序中,我们需要先读入数据,然后排序,排序完成后再写入磁盘。因为我们没法读一个正在写的数据块,所以我们只需要在不同的数据块读和写就行了。
- 对于 k-way 中的每一路,我们都提供两个 input buffer,一个用于写,一个用于排序。当排序 buffer 空了的时候,就和读满了的 input buffer 交换,无缝衔接继续输出。于此同时,刚刚被交换过去的 buffer 则可用于继续读入。因此,如果我们执行 direct k-way merge,就需要 2k 个 input buffer(这里强调 direct 是因为,如果使用 iterative 的话,input buffer 只需要 4 个)。
- 而对于输出,我们只需要 2 个 output buffer 交替使用即可,一个用来接收来自排序算法的输出,一个用来将数据写入磁盘。
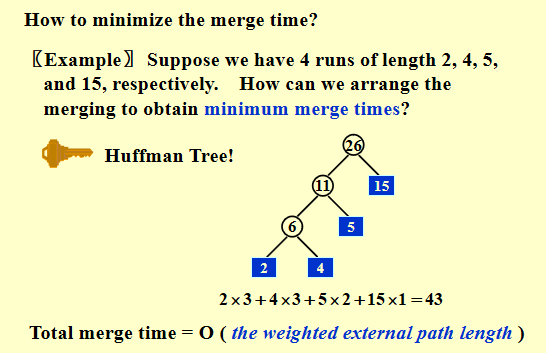
知识5–利用哈夫曼排序来最小化归并时间(针对两两归并)
![hafuman]()
期中刷题的一些记录
16-17期中模拟(-3-6)
ex1 关于旋转
![banqi1]()
解释:首先zig zag zig-zag操作就是针对于splay树而言,当进行多次旋转时,节点深度通常会大约减半。ex2 b+树的相关知识
![banqi2]()
解释:首先是b+树的order理解不足,在我们前面基础知识部分提到的M就是order知识1
在红黑树中,内部红节点的度数不可能为1.知识2 AVL(薄弱)
- AVL树中height的定义:ppt中the height of an empty tree is defined to be -1.
- The balance factor BF(node)=$h_{L}-h_{R}$
- 调整平衡时的具体操作有一点点忘却啦.(尤其是两次旋转时都是对于发现出错的下面最近的两个节点与其操作)
知识3 二向队列合并的具体代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
BinQueue BinQueue_Merge( BinQueue H1, BinQueue H2 )
{ BinTree T1, T2, Carry = NULL;
int i, j;
H1->CurrentSize += H2-> CurrentSize;
for ( i=0, j=1; j<= H1->CurrentSize; i++, j*=2 ) {
T1 = H1->TheTrees[i]; T2 = H2->TheTrees[i];
switch( 4*!!Carry + 2*!!T2 + !!T1 ) {
case 0:
case 1: break;
case2:
H1->TheTrees[i]=T2;H2->TheTrees[i]=NULL;Carry=NULL;break;
case 4: H1->TheTrees[i] = Carry; Carry = NULL; break;
case 3: Carry = CombineTrees( T1, T2 );
H1->TheTrees[i] = H2->TheTrees[i] = NULL; break;
case 5: Carry = CombineTrees( T1, Carry );
H1->TheTrees[i] = NULL; break;
case 6: Carry = CombineTrees( T2, Carry );
H2->TheTrees[i] = NULL; break;
case 7: H1->TheTrees[i] = Carry;
Carry = CombineTrees( T1, T2 );
H2->TheTrees[i] = NULL; break;
} /* end switch */
} /* end for-loop */
return H1;
}
CombineTrees( BinTree T1, BinTree T2 )
{ /* merge equal-sized T1 and T2 */ if ( T1->Element > T2->Element )
/* attach the larger one to the smaller one */return CombineTrees( T2, T1 );
/* insert T2 to the front of the children list of T1 */
T2->NextSibling = T1->LeftChild;
T1->LeftChild = T2;
return T1;
}
15-16期中模拟(-3-3-5-4)
- 知识1 动态规划与多项式解决问题并不存在相关性
- 知识2 红黑树的插入后调整的三种情况
- LL:左左,此时只需要对u进行右旋即可,然后两个儿子均为红
- LR:旋转后转化为第一种情况
- 父亲和父亲兄弟与自己:先把父亲和父亲兄弟染黑,父亲父亲染红再观察。
- 知识3 一个操作的均摊操作与平均时间:
平均时间 是针对算法在所有可能输入上的平均性能,考虑了输入分布或随机性的影响。它是一种概率性分析,往往需要假设输入的分布是已知的
均摊时间 则是针对一系列操作的总时间进行分析,并通过分摊成本得出单个操作的平均时间。它不依赖于输入的概率分布,而是通过考虑整体操作序列的代价,来平均每次操作的开销。 - ex1 红黑树的黑高
![banqi3]()
解释:在红黑树中我们存在一个结论$bh(u)>=\frac{1}{2}h(u)$,$2^{2*bh(u)}>=2^{h(u)}>=u$,$sizeof(x)>=2^{bh(x)}-1$ 与题目描述不符 - ex2 分治的时间复杂度
![banqi4]()
解释:$T(N)=4*T(N/5)+O(logN)$,$T(N)=aT(N/b)+O(N^{k}(logN)^{p})$,$a>b^{k},O(N^{log_{b}a}),a=b^{k},O(N^{k}(logN)^{p+1}),else,O(O(N^{k}(logN)^{p}))$
王灿期中 24-25秋冬
- 知识1 $\alpha,\beta$剪枝操作
- 知识2 红黑树的删除操作(之前复习未覆盖)
- 知识3 b+树的时间复杂度(确实是容易被忽视的一个点)
- 知识4 有关动态规划的一道题目
![banqi8]()
解释:这一道dp也是leetcode上面经典的一道二维dp的题目,我们的状态转化方程其实本质上基于题干上面的三个操作,按照题干进行定义,when $word1[i]=word2[j],dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],dp[i-1][j-1]-1)$
$word1[i]!=word2[j],dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],dp[i-1][j-1])$ - 错误点1 对于堆的均摊操作的考虑
![banqi6]()
解释:只有先记结论(lz暂时没有给出严格证明) - 错误点2 分治的主方法未能记住并灵活运用(正如15-16期中模拟一样)
![banqi5]()
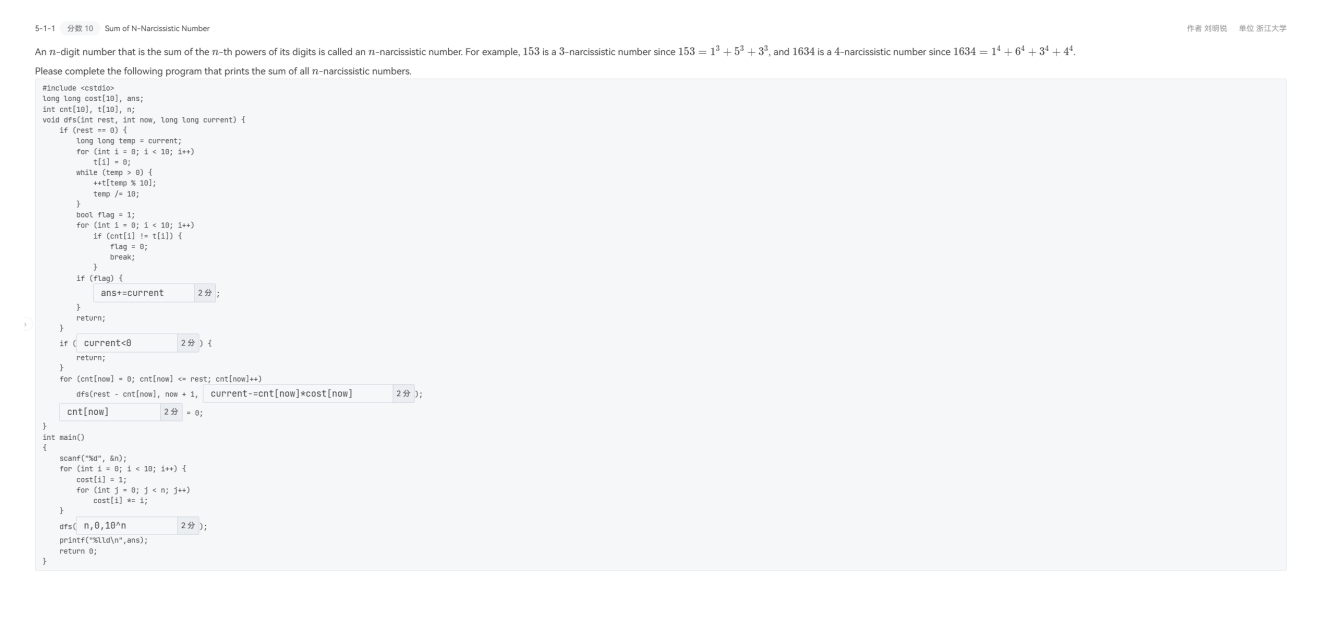
解释:$T(n)=4*T(n/4)+log(n)$,we can get $a=4,b=4,k=0,p=1,a=b^{k},O(N^{k}(logN)^{p})$ - 错误点3 程序填空题(个人认为这个题的难度在期中应该是T0存在)
![banqi7]()
解释:首先我认为我们需要弄明白各个数组的含义,首先在main函数中可以知道,cost[]代表在这个n的情况下,对应的$i^{n}$;current为当前待判断的数看它是否是n-narcissistic number;t[]则是存储current的各个位数的相应数字;
bjj 期中24-25秋冬
- 错误点1 二向队列的构建
![banqi9]()
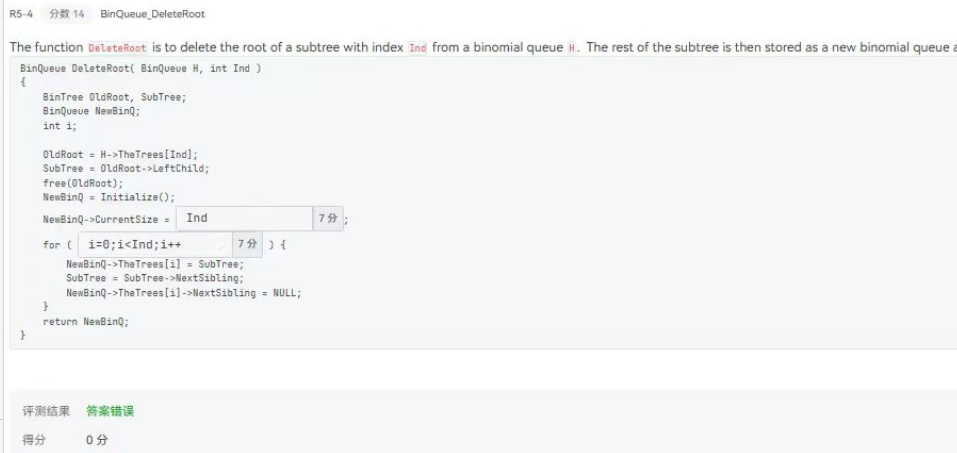
解释:这道题我觉得最主要的是概念问题,首先binomial queue是由binomial tree组成,而subtree又是组成binomial tree,在形成一颗binomial tree时是按照层次结构,并不能简单的说是按照increasing number。 - 错误点2 二向队列的删除
![banqi11]()
解释:首先我觉得这道题出错最可能的原因是不太清楚二向队列的各个参数的具体含义。首先currentsize代表是整个二向队列的所有的节点数量,而不是binomial tree的数量!,并且这一道题不知道是否存在math库所以我们采用移位操作$Ind<<1-1$,而在下面的一个空主要是对于二向树的结构的了解不够深,我们的最左的子树其实是size最大的则我们的循环语句$for(i=Ind-1;i>=0;i–)$ - 知识点1 渐进上限
![banqi10]()
解释:首先对于题干中的中文解释其实就是渐进上限,就我自己思考而言,当n足够大时在一定程度上可以减弱“17”的效果,这样可以运用主方法,但是较为严谨的还是利用递归树来看待这个分治复杂度,$T(n_{i})<=n+17$(递归树中每一层的时间复杂度的上限)
ads期末刷题记录
2023-2024春夏
- 知识点1–贪心的特点
overlapping sub-problems其实是动态规划的特点,意思是重复计算。例如斐波拉契问题。 - 知识点2–并行算法
其实并行算法对于maximum finding的优化的Doubly logarithmic Paradigm包含我之前知识点的两种优化方式。
2020-2021春夏
2020-2021判断
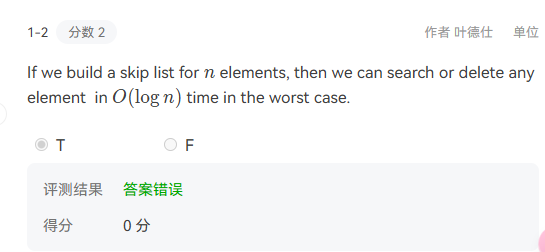
- 知识点–skip list
![skip]()
解释:这一道题确实是自己的知识问题。跳表的平均时间复杂度为$O(logN)$,跳表的空间复杂度为$O(N)$,但是最坏的时间复杂度为$O(N)。 - 知识点–skew heap
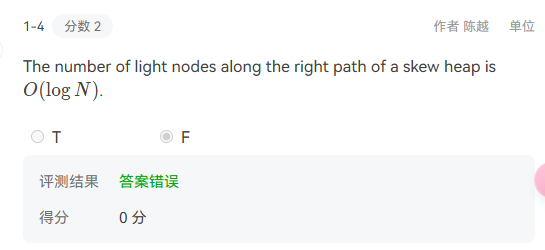
![skew]()
解释:这一道题是当时没有认真系统复习,对于skew heap的知识遗漏。因为我们证明skew heap的摊还时间的最后一个不等式其实就是用到了light node的数量为$O(log n)$的结论,而这一个结论可以通过归纳假设证明。 - 知识点3–回溯
![back]()
解释:这一道题是自己的对于解空间的理解不够深入,其实前面的一次作业题也提到了解空间(解空间(Solution Space)是一个问题所有可能解的集合。在算法和优化问题中,解空间通常指的是可以通过穷举或搜索所有可能解所构成的空间。)我们的回溯其实就是在解空间中寻找解,但是解不会变化。 - 知识点4–树的定义与霍夫曼
![tree]()
解释:fds的一些理论有点忘记了。完全二叉树是一种二叉树,具有以下性质:每一层的节点都尽量靠左对齐。除了最后一层外,每一层的节点都是满的。最后一层的节点从左到右连续排列,但可以不满。满二叉树是一种二叉树,具有以下性质:每个节点要么是叶子节点,要么有两个子节点。所有叶子节点都在同一层。所以很容易知道这句话是正确的。而完美二叉树是最完美的完全二叉树,兼具完全二叉树和满二叉树的性质。 - 知识点5–local search
![local]()
解释:这道题纯粹是理解问题。但在某些复杂优化问题中,局部改进未必能够一次找到局部最优解。例如,启发式算法(如模拟退火)需要多次操作逐步接近最优解。
2020-2021选择
- 知识点–随机
![suiji]()
解释:这一道题为随机化求期望,A很简单直接算就行;对于B选项我觉得最好先要考虑某个特定的空盒子最终空的概率,对于这个盒子,$P=(1-\frac{1}{m})^m=e^{-1}$,则最终的空盒子数目为$\frac{m}{e}$;对于C选项,现在我们限定条件一个盒子只能放一个球。此时我们被拒绝的形式如下:$\sum_{i=1}^{m}(1-\frac{1}{m}(1-\frac{1}{m})^i)=m-\sum_{i=1}^{m}(\frac{1}{m}(1-\frac{1}{m})^i)$等比数列求和可以得到正确答案。D选项暂时不计算了。 - 知识点–算法分析
![max]()
解释:这一道题是设计一个时间复杂度最小的算法。因为两个数列A和B其实已经排好序了,我们假如首先二分A,二分B,那么我们就能知晓此时的指针所指的两个数的位次,然后再分别进行二分。 - 知识点3–external sorting
![external]()
解释: - 知识点4–approximation
![approxi]()
解释:我觉得这一道题目是我对选项的理解有误,首先题干是给出了FF与NF的近似度的具体值,然后对于这一个特殊样例,NF其实就是它的最坏情况,但是FF能够达到1,说明FF的近似比得到改善。我将improved理解成增加(lz英语不好的缘故)。 - 知识点5–AVL tree
![avl]()
解释:对于这种类型的题目一定不要着急,lz的第二套模拟题吃了大亏。
1:AVL 树是一种高度平衡的二叉搜索树(height-balanced binary search tree),其每个节点的平衡因子(左右子树高度差)只能是1,−1,0。题目中提到平衡因子“只能是 0 或 1”,忽略了 −1 的情况。
2:满二叉树
3:AVL 树不是严格平衡(strictly balanced)的,它是高度平衡(height-balanced),正确。
4:在伸展树(splay tree)中,每次访问某个节点后,都会将该节点旋转到根节点。即使只是查找操作,也需要执行伸展操作。因此,不执行伸展以减少操作成本是不符合伸展树定义的。错误。
5:这个选项我也有疑问,gpt的回答是splay用词不恰当,因为splay伸展操作是要操作节点到根部的。
6:伸展树的伸展操作会将访问路径上的节点“提上来”,减小其深度。尽管不是精确减半,但总体趋势是显著减少路径上的节点深度。
2020-2021编程题
这一道编程题是一个典型的动态归化,其实就是有两个序列,然后组队乘积之和最大,并且两两之间组队的连线不交叉,这就意味着我们可以利用动态归化,本质上就是在线操作。
我们利用二维数组进行解决,用dp来存储状态,然后利用动态规划进行求解,dp$[i][j]$表示A数组从0到i,B数组从0到j这一个局部状态的最大乘积之和。
状态转移方程:
1
2
3
4
5
6if(dp[i-1][j-1]+bread[i]*cream[j]>dp[i][j-1]&&dp[i-1][j-1]+bread[i]*cream[j]>dp[i-1][j])
dp[i][j]=dp[i-1][j-1]+bread[i]*cream[j];
else if(dp[i][j-1]>dp[i-1][j])
dp[i][j]=dp[i][j-1];
else
dp[i][j]=dp[i-1][j];
2019-2020春夏
2019-2020判断
- 总结:有两道题是很能避免的。
- 知识点1–external sorting
![external2]()
解释:external sorting确实是我较为薄弱的部分,我这一道题太执着于结论而忽略了后半段话。在外部排序中,我们减小passes的方式通常是使用k-way merge的操作。而buffer只是为了处理并行算法让写和读操作同时进行。 - 知识点2–leftist heap and skew heap
![skew2]()
解释:我目前还不知道答案的意义。 - 知识点3–倒排索引
![daopai]()
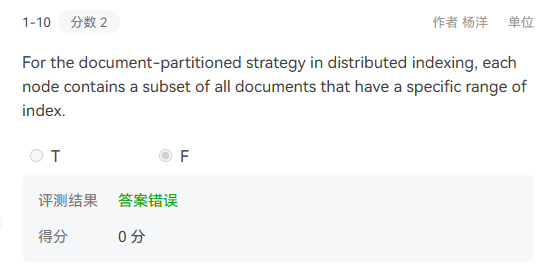
解释:虽然对于倒排索引我也学的很八股但是这道错误,我觉得是读题太快导致的,今天下午太着急了!题目讨论的是 Document-Partitioned Strategy:
文档被划分到不同节点中。
每个节点存储与自己负责的文档相关的索引。
“特定范围的索引”表明每个节点的负责范围是按照文档来划分的。
所以题干强调的subset是正确的。 - 知识点4–红黑树
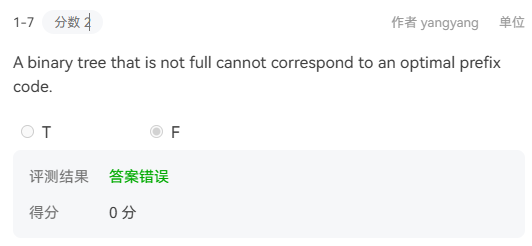
![honghei]()
解释:这种基础题真不能错了。红黑树的定义是到所有NIL节点的路径的黑高是相同的,很明显14到16的右儿子这条路径的黑高要短,说明这棵树不符合红黑树的定义。 - 知识点5–NP
![np]()
解释:这个题其实仔细分析也能分析,因为我们的dijsktra都是可以在多项时间内解决shortest path问题,所以本来就是p类问题,当p和np相等说它是np也一样。
2019-2020选择
- 总结:这一次的选择正确率太低,而且错了几道数据结构的题目,基础还要巩固。
- 知识点1–splay tree
![splay2]()
解释: - 知识点2–skew heap
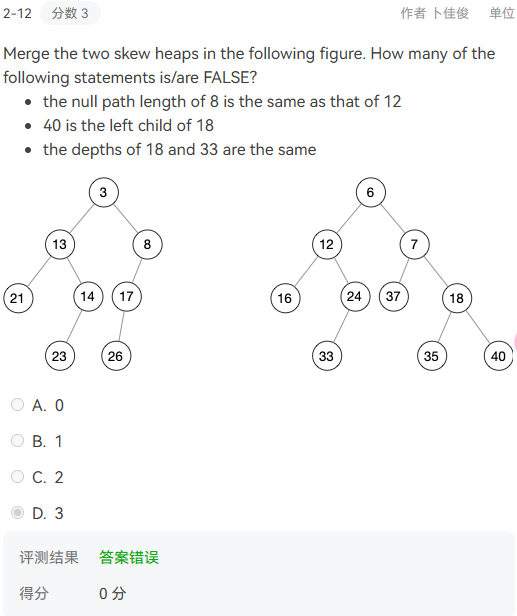
![skew3]()
解释:首先第一点题没看清,FALSE!!今天感觉整体太着急,就是没有进入做题的状态。但是我自己判断3个都是对的,标准答案为3个正确(因为我参考的另一个同学的题干和这个题不一样)。但是在做这道题目是虽然自己选项判断的是对的,但是当时在skew heap的最后的操作有一些疑问。后来发现,假如我们已经到了最底部:右节点为空和另外一颗子树合并,那么这一颗子树本身的左右子树也要互换!但是后来我仔细分析了ppt提供的代码,我目前对这个题保持疑问。后来和stone佬讨论发现递归实现很容易出错,最好采用迭代来解决skew heap,并且一个方便记忆的方法是对于递归操作(合并交换前在最右路径的节点,交换后一定在最左路径)。 - 知识点3–avl tree(暂定)
解释:因为这道题和上一道一样看错题,我不知道正确答案究竟是怎么样的。 - 知识点4–贪心
![tanxin]()
解释:这一道题目在做题时确实没有找出反例,也是时间关系。后来编写了一个程序发现在n=20时找到了反例greedy1不是最优的而greedy2是最优的。
Greedy1 是为单个房间找到最大活动数的算法,但不一定能优化 最小房间数。它忽略了跨房间的全局约束,因此不是解决最小房间数问题的最优解。
Greedy2这是一个典型的调度问题解法,类似于“区间图着色问题”。保证了房间数的最小化,是一种有效的最优贪心策略。 - 知识点5–NP
![np2]()
解释:这种题考试只能猜测了。其实D选项课上也大概讲过,但是自己并没有特别理解,主要记忆贪心的2近似解法了,详细见下面这张图片。![np4]()
B:这个陈述也是正确的。最小度数生成树问题是一个NP-hard问题,特别是当目标是找到一个最大度数为2的生成树时,这实际上是寻找一个哈密顿回路的问题,已知是NP-complete的。
C:这个陈述是错误的。最小度数生成树问题是一个NP-hard问题,目前没有已知的多项式时间近似算法能够保证近似比小于3/2。实际上,这个问题的近似难度是已知的,我查阅文献发现最好的情况最小度数为1+$\delta$ - 知识点6–NP
![np3]()
解释:其实我选错是对第三个statement理解有误,因为如果X能够被确定性地在多项式时间内解决,说明NP=P;并且目前还没有被证明NP=P,所以There is no polynomial time algorithm for X.
2019-2020 编程
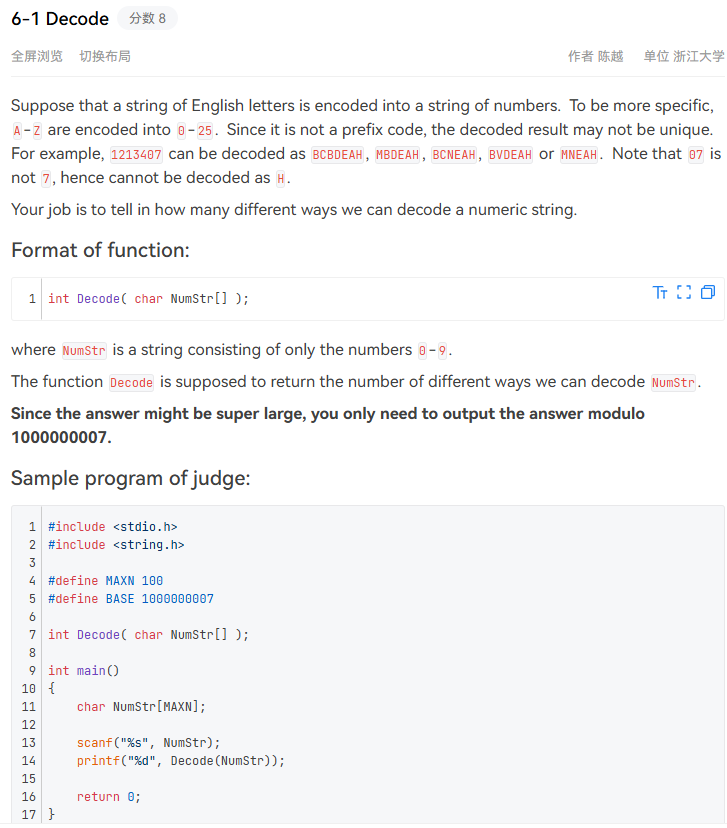
基本的解答思路如下:
我当时出错的部分原因可能是状态转移方程的判断条件写错了两个都用的NumStr(i-1),否则可能还会多几分吧。
1 | |
2018-2019春夏
2018-2019判断
- 知识点1–倒排索引
![daopai2]()
解释:注意document分布和query分布的评判标准
document:只检索前面x个按权重排序的文档
1.1 对于布尔查询无效
1.2 会遗漏一些重要的文档,因为有截断
query:把带查询的terms按照出现的频率升序排序 - 知识点2–随机化
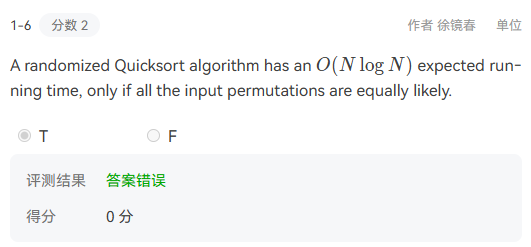
![suiji2]()
解释:input permutations–输入排列。我们的随机的快排与输入排列无关,所以无论怎样改变都不会影响时间复杂度。 - 知识点3–外部排序
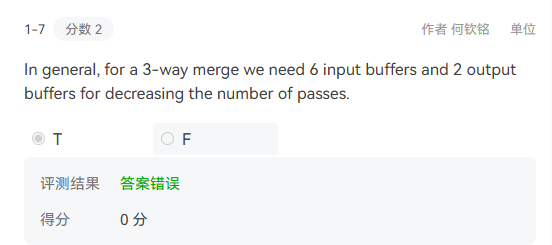
![external3]()
解释:我感觉是对simple k-way merge的理解不恰当。后来发现是因为这里忽略了公式最开始的1.
2018-2019选择
- 知识点1–近似比
![approxi2]()
解释:这道题还是没有认真分析各个选项之间的关系。当$\alpha \gt \frac{1}{2}$时:因为我们知道NF的近似比最多为2,而此时我们确实能举出例子。比如一个物品大小为0.75,一个物品大小为0.33当它们交替存在在序列中时,假设序列长度为2n,此时NF=2n,OPT=3n/4,当我们的n较大时此时若$\rho=2\alpha$不等式不会成立。 - 知识点2–倒排索引
![daopai3]()
解释:我感觉这种题是不应该出错的。还是对题目的理解出了问题,这是一个垃圾信息检测系统,则我们肯定是希望我们的检测的垃圾信息的精度要高,从而方便我们的清理(recall感觉是那种防患于未然)。