普通物理学I(H)

普通物理学1[H]

期中总结

ex1(微元法)

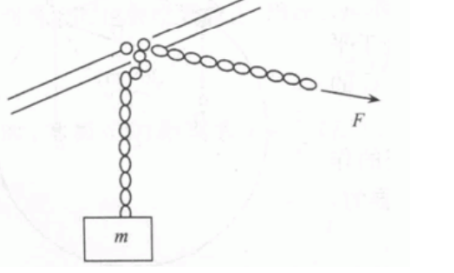
hint:微元法

$\int_{0}^{5/2\pi}$$d\phi$=$1/u$$\int_{mg}^{T}$$dT$

ex2(多普勒效应)

$f^`=f*(v+vd)/(v-vs)$

ex3(科里奥利力)

期末碎碎念啦

热力学

• 熵

1. 定义：$\int_{}^{}$ $\frac{dQ}{T}$

2. 性质：与路径无关，则我们可以在解决问题时构造可逆路径，只需要初末状态一致

3. 一些例子

   free expansion：$\delta$S=$\int_{}^{}$ $\frac{PdV}{T}$=$\int_{}^{}$ $\frac{nRdV}{V}$=nRln$\frac{Vf}{Vi}$

   对于理想气体的普适情况：dS=$\frac{1}{T}$(dU+PdV)

   S=S0+$\int_{}^{}$ $\frac{dU}{T}$+$\frac{PdV}{T}$=S0+Cvln$\frac{T}{T0}$+nRln$\frac{V}{V0}$

4. 在微观领域（玻尔兹曼熵）

   s=kblnw w(一个特定宏观状态下的微观状态数量)

• 热力学第二定律

1. otto cycle

   定义热机效率=$\frac{W(net)}{Qh}$
   而奥托循环由两个恒定体积过程与一个绝热过程组成
   则e=1-$\frac{Td-Ta}{Tc-Tb}$

2. 卡诺机
   卡诺机由两个等温过程与两个绝热过程构成
   绝热：Q=W=NkbTln $\frac{Vf}{Vi}$
   可以得到$\frac{Qc}{Qh}$=$\frac{Tc}{Th}$
   e=1-$\frac{Tc}{Th}$

3. 再探究绝热过程
   可以得到 T$V^{\gamma-1}$=const
   其中$\gamma$=$\frac{cp}{cv}$=1+$\frac{nkb}{cv}$=1+$\frac{2}{f}$
   $c_p=c_v+R$(没有n的原因是因为这两个量的本身定义便是单位温度释放热量)

• 热力学第一定律

1. 核心公式：$\delta$U=Q-W
   做功:W=$\int^{}{}$PdV

2. 热传递（傅里叶定律）
   $\frac{dQ}{dT}$=-k(热导系数)$\frac{dT}{dX}$A(横截面积)

3. 平均自由程（在一定的条件下，一个气体分子在连续两次碰撞之间可能通过的各段自由程的平均值，微粒的平均自由程是指微粒与其他微粒碰撞所通过的平均距离）
   l=$\frac{kbT}{\sqrt{2}\pi d^{2}p}$

4. 讨论一些微观量
   核心方程(nRT=N$k_B$T)
   范德华方程：(p+$\frac{aN^{2}}{V^{2}}$)(V-Nb)=N$k_{B}$T
   临界条件($P_c=\frac{a}{27b^{2}},V_c=3nb ,T_c=\frac{8a}{27bR}$)
   $U_{内能}$=Nf(自由度)$\frac{k_{B}}{2}$T$(一般平动自由度为3；单原子转动自由度为1，双原子为2，线性多原子为2，其他为3；振动自由度为3N_{原子数目}-平动自由度-转动自由度)$
   均方根速度:$v_{rms}$=$\sqrt{\frac{3k_{B}T}{m}}$
   最概然速率:$v_{p}$=$\sqrt{\frac{2k_{B}T}{m}}$
   平均速度: $v_{p}$=$\sqrt{\frac{8k_{B}T}{m\pi}}$

5. 热膨胀
   $\delta$L=$\alpha$$L_{0}$$\delta$T
   $\delta V=\beta V_{0}\delta T$ 可以推出$\beta$=3$\alpha$

相对论

• 洛伦兹变换(最核心)

1. 核心公式
   $t=\frac{t^{‘}}{s}+\frac{v}{sc^{2}}x^{‘}$
   $x=\frac{v}{s}t^{‘}+\frac{x^{‘}}{s}$
   $y=y^{‘}$
   $z=z^{‘}$
   =>
   $t^{‘}=\frac{t}{s}-\frac{v}{sc^{2}}x$
   $x^{‘}=-\frac{v}{s}t+\frac{x}{s}$
   其中$s=\sqrt{1-\frac{v^{}2}{c^{}2}}$
   且带上标的参考系相对于不带上标的参考系沿x轴正向运动

2. 利用洛伦兹变换进行尺缩与时间放缓的推导

   尺缩效应：
   假设一根棍静止放在轨道上，另外一个体系相对于这个静止轨道运动，那么我们现在考虑在这个的运动的体系中观测者测量这跟静止木棍的长度。则观测者需要记录${x_{0}}^{‘}$,${x_{1}}^{‘}$,则观测者测得的木棍长度为${x_{1}}^{‘}$-${x_{0}}^{‘}$=$\frac{x_{1}-x_{0}}{s}$+$\frac{vt_{0}-vt_{1}}{s}$其中因为测量过程在宏观上实在测量者一个瞬间发生，即${t_{1}}^{‘}={t_{0}^{‘}}$,
   则根据推导的等式可以知道，$t_{0}-t_{1}=\frac{v}{c^{2}}(x_{0}-x_{1})$
   代入等式可以得到:观测者测得的木棍长度=sL，则得到了尺缩效应的结论
   时间延缓:
   则我们考虑两个相同发生的事件，计算两个事件发生的时间间隔分别在静止系和运动系之间的差异，从而得到结论。在静止系K上两个事件的距离差异为vt,时间差异为t.而在运动系中，两个事件的距离差异为0，时间差异为$t^{‘}$,由下面的“双曲线等式”容易推出:$t^{‘}=st$

3. 一个简单的推导
   利用上述的洛伦兹变换，可以证明如下等式：
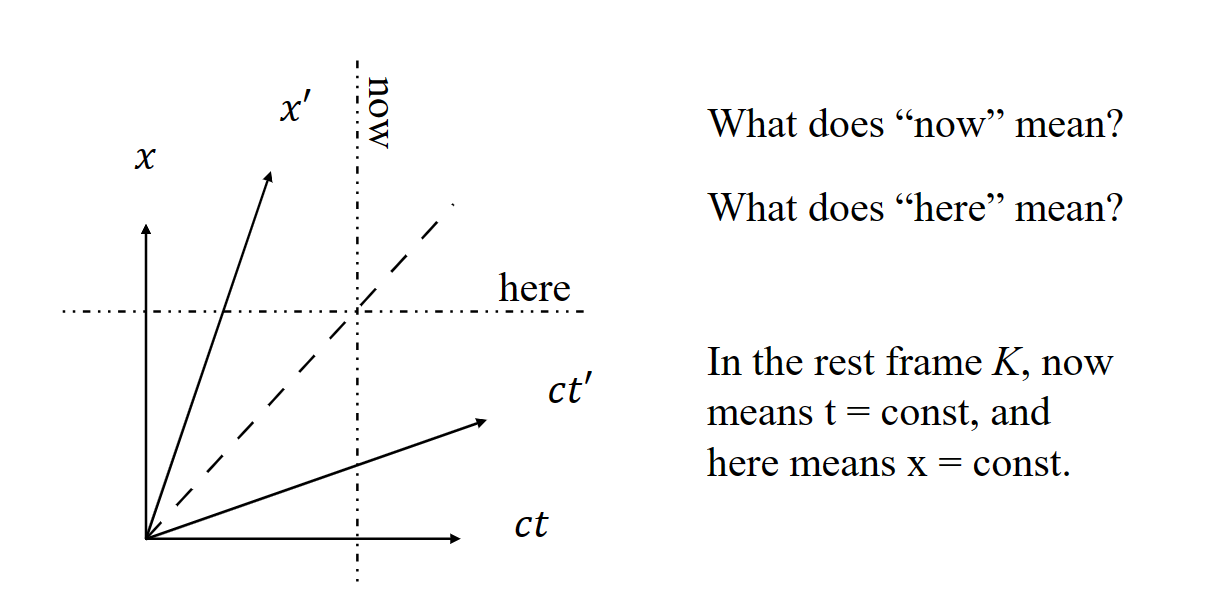
   $c^{2}t^{2}-x^{2}={c^{‘}}^{2}{t^{‘}}^{2}-{x^{‘}}^{2}=s^{2}$

4. minkowski 图
   
   需要注意的是：因为这个图的倾斜的性质，且我们设两个坐标之间的夹角为$\theta$,$\tan \theta$=$\beta$=$\frac{v}{c}$,则会存在单位的协变性，当长度为“1”时，在图中的长度为$\sqrt{\frac{1+{\beta}^2}{1-{\beta}^2}}$,则亦能在minkowski图上面得到长度收缩的结论。

• 在运动学与能量方面的修正

1. 速度变换
   利用洛伦兹变换求导即可得到速度变换公式

2. 动量与能量修正
   动量:$p=\frac{mu}{\sqrt{1-\frac{u^{2}}{c^{2}}}}$(其中u并不是相对于一个参考系的速度而是绝对速度)
   能量:$k=\frac{mc^{2}}{\sqrt{1-\frac{u^{2}}{c^{2}}}}-mc^{2}$
   并且我们注意到修正公式与洛伦兹变换的推导有很多异曲同工之处（“双曲线等式”）Likewise,$ m^{2}$is an invariant, which is independent of the frame of reference. P = (E/c, px, py, pz) is often called the energy-momentum 4-vector, or the 4-momentum.

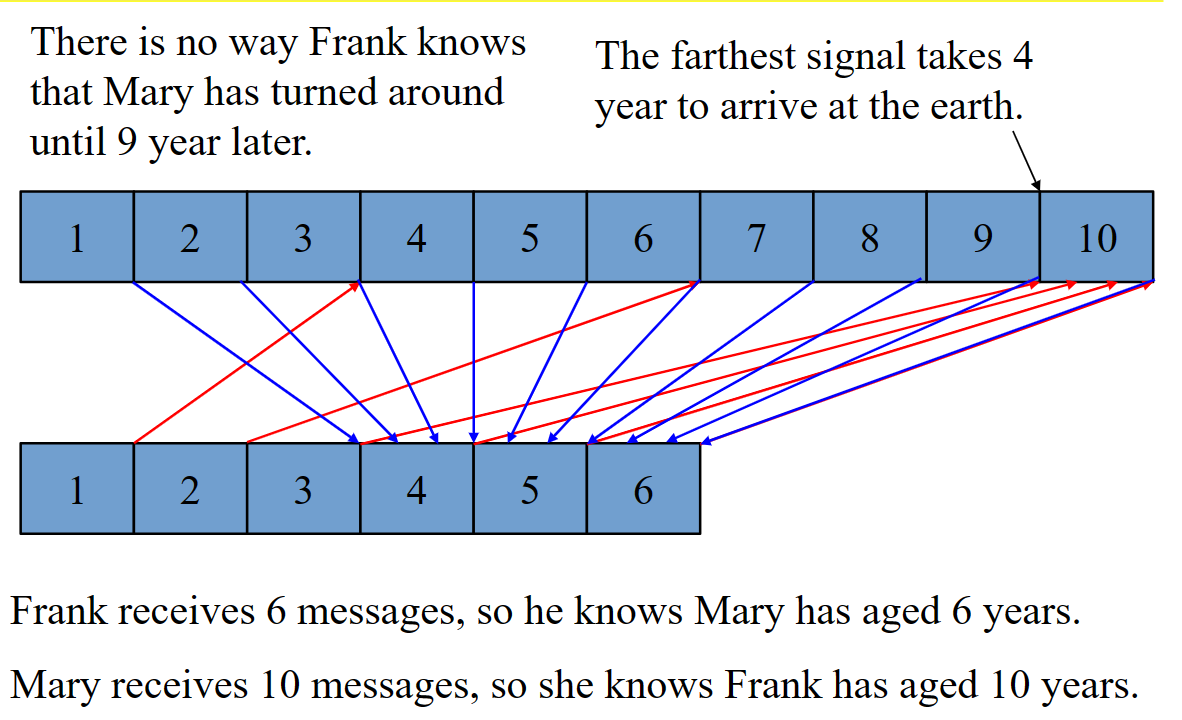
• 相对论下的多普勒效应(孪生兄妹悖论)
  一般的多普勒效应:$f^{‘}=\frac{v+v_0}{v-v_s}f$
  相对论下的多普勒效应:$f=\sqrt{\frac{1+v/c}{1-v/c}}f_0$
  ($f_0$是源的频率$f$是接收者的频率,v是源相对于接收者的速度)
  但是若源接近观测者则$\beta$被视作负值
  这里是对悖论的解释
  

我觉得相对论下的多普勒效应能从另一角度说明相对论的正确性